Radiofrequency tissue ablation is a medical procedure that uses targeted heat for a variety of medical purposes, including killing cancerous cells, shrinking collagen, and alleviating pain. The process involves applying mid- to high-frequency alternating current directly to the tissue, raising the temperature in a focused region near the applicator. We can simulate this process with COMSOL Multiphysics and the AC/DC and Heat Transfer modules. In today’s blog post, we will go over some key concepts for modeling this procedure.
What Is Radiofrequency Tissue Ablation?
Whenever an alternating electric current (or a direct current, for that matter) is applied to living tissue, there will be heat generation and temperature rise due to Joule heating. The ability to target this heat to specific localized tissue areas is a key advantage of the radiofrequency tissue ablation technique.
In one of many medical applications, a cancerous tumor is a localized target. Using heat, the temperature of the area is raised to kill the cancer cells. Alternating current is used (rather than direct) to avoid stimulating nerve cells and causing pain. When alternating current is used, and the frequency is high enough, the nerve cells are not directly stimulated.
To understand how we can model this process, let’s examine the figures below, which show some of the key concepts of this technique.
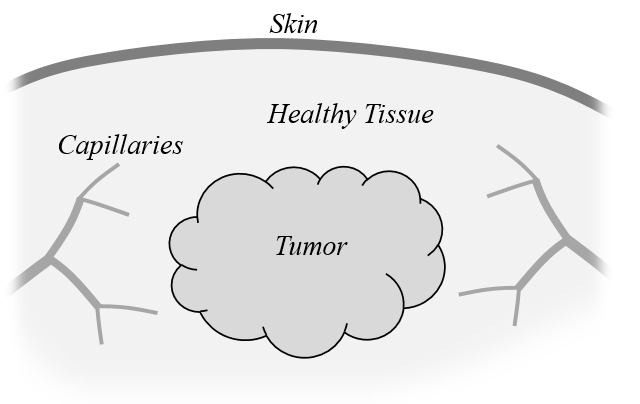
A tumor within healthy tissue. Capillaries perfuse blood through the tissue and tumor.
When an undesirable tissue mass is identified, such as a tumor, a doctor can use either a monopolar or bipolar applicator to inject current into and around the tumor. The current comes from a generator and varies sinusoidally in time. Frequencies of 300 to 500 kHz are common, although the procedure can use much lower frequencies.
There are a wide variety of electrode configurations ranging from flat plates and single needles to a cluster of needles, depending on the desired shape of the heated domain and how the doctor will access the tissue. One common class of applicator is deployed through the circulatory system by using a long, flexible catheter and then extending a set of needles from the distal end into the tissue to be heated.
A monopolar applicator is made up of a needle and patch applicator, whereas a bipolar applicator consists of two needle electrodes. More than two applicators and other applicator configurations are also possible. By convention, one electrode is called the ground, or reference, electrode. The voltage applied at the other electrode is with respect to this ground.
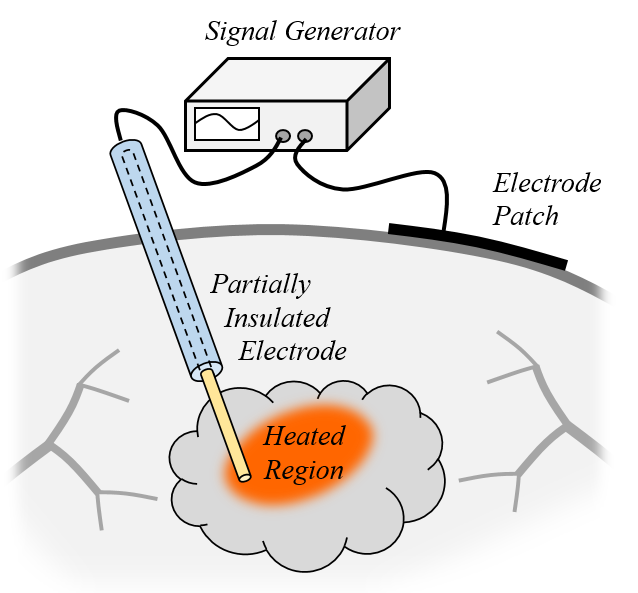
A monopolar radiofrequency applicator and a patch electrode on the skin’s surface.
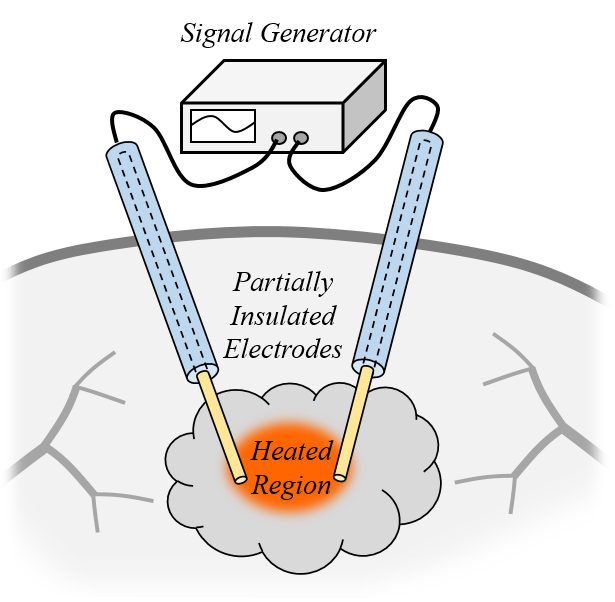
A bipolar applicator primarily heats the region between the electrodes.
An engineer designing one of these devices has a complicated problem to solve. The shape of the heated tissue depends on the shape and number of electrodes; which part is insulated and which is not; and ultimately, the thermal energy absorption distribution of the nearby tissue over time.
The sharp, pointed ends of the needle electrodes complicate the design process, since they lead to high current densities and thus uneven temperature rise along the needle. For the cancerous tumor application, the goal is to kill the undesirable tissue mass and leave the surrounding healthy tissue unharmed. For shrinking collagen, the goal is still to heat tissue, but to avoid any possibility of damaging cells. COMSOL Multiphysics simulation streamlines and shortens this process.
To properly model this procedure, we must build a model of the electric current flow through the tissue as well as the heat generation and temperature rise. Let’s explore these steps.
Analyzing Joule Heating and Current Flow
We begin by examining the typical material properties of both the applicator and living tissue and discuss how these materials behave at an operating frequency of 500 kHz. The table below shows the representative electrical conductivity, \sigma; relative permittivity, \epsilon_r; skin depth, \delta; and complex-valued conductivity, (\sigma+j\omega \epsilon_0 \epsilon_r) at 500 kHz.
Although there is a variation to the electrical conductivity and relative permittivity of different tissues, for the purposes of this discussion, we will approximate the human body as having the properties of a weak saline solution. The actual properties of tissue do not vary by much more than one order of magnitude from this value, while the conductivity of the electrode and insulator are over five orders of magnitude larger or smaller.
| Electrical Conductivity (S/m) | Relative Permittivity | Skin Depth at 500 kHz (m) | Complex Conductivity at 500 kHz (S/m) | |
|---|---|---|---|---|
| Metal Electrode | 106 | 1 | ~10-4 | 106 + j 4 x 10-6 |
| Polymer Insulator | 10-12 | 2 | ~1010 | 10-12 + j 9 x 10-5 |
| “Average” Human Tissue | 0.5 | 65 | 1 | 0.5 + j 0.0003 |
We compute the skin depth to decide if we need to compute the magnetic fields and any heating due to induced currents. At 500 kHz, the electrical skin depth of the human body is on the order of one meter, while the heated regions have a typical size on the order of a centimeter. Hence, we can make the approximation that heating due to induced currents in the tissue is negligible and need not be calculated. Note that this approximation will not be valid if some small pieces of metal exist within the tissue, such as a stent within a nearby blood vessel.
We can also see from the magnitude of the complex conductivity in the above table that the electrodes are essentially perfect conductors when compared to tissue. Similarly, the polymer insulators can be well approximated as perfect insulators when compared to human tissue.
This information lets us choose the form of our governing equation. Under the assumption that magnetic fields and induction currents are negligible and operating at a constant frequency, we can solve the frequency-domain form of the electric currents equation. Further assuming that the human body itself does not generate any significant currents, the governing equation is:
which solves for the voltage field, V, throughout the modeling domain. The electric field is computed from the gradient of the voltage: \mathbf{E} = -\nabla V. The total current is \mathbf{J} = (\sigma+j\omega \epsilon_0 \epsilon_r) \mathbf{E} and the cycle-averaged Joule heating is Q = \frac{_1}{^2} \Re (\mathbf{J}^* \cdot \mathbf{E} ).
Since the conductors are essentially perfectly conducting compared to the tissue, we can omit these domains from our electrical model. That is, we can assume that all surfaces of the metal electrodes are equipotential. This is reasonable if the equivalent free-space wavelength (\lambda = c_0/f = 600m) is much larger than the model size. When using the AC/DC Module, we can use the Terminal boundary condition to fix the voltage on all surfaces of the electrode. The Terminal boundary condition can specify the applied voltage, total current, or total power fed into the boundaries.
It is reasonable to ask why the conductor is omitted, for there is indeed some finite heat loss within the electrode itself. The heating within the electrode, however, is many orders of magnitude lower than in the surrounding tissue. Although the currents in the conductor can be quite high, the electric field (the variation in the voltage along the electrode) is quite small, hence the heating is negligible.
Similarly, since the insulators are essentially perfect, these domains can also be eliminated from the electrical model. In the insulators, the electric fields may be quite high, but the current is essentially zero, which again means negligible heating. The Electric Insulation boundary condition, \mathbf{n} \cdot \mathbf{J} = 0, can be applied on the boundaries of the insulators and implies that no current (neither conduction nor displacement currents) passes through these boundaries. There is one caveat to this: If the electrodes are completely enclosed within the insulators, then there will be significant displacement currents in the insulators and these domains should be included in the model.
On the exposed surface of the skin, the Electric Insulation boundary condition is also appropriate. However, if there is an external electrode patch applied to the skin’s surface, then current can pass through the skin to the electrode. The conductivity of skin is lower than that of the underlying tissue, and this should be modeled. However, we may not want to model the skin explicitly as a separate domain. In such cases, the Distributed Impedance boundary condition applies the condition \mathbf{n} \cdot \mathbf{J} = Z_s^{-1}(V-V_0), where V_0 is the external electrode voltage and Z_s is the equivalent computed impedance of the skin.
A schematic of such a model is shown below, with representative material properties and boundary conditions. Now that the electrical model is addressed, let’s move on to the thermal model.
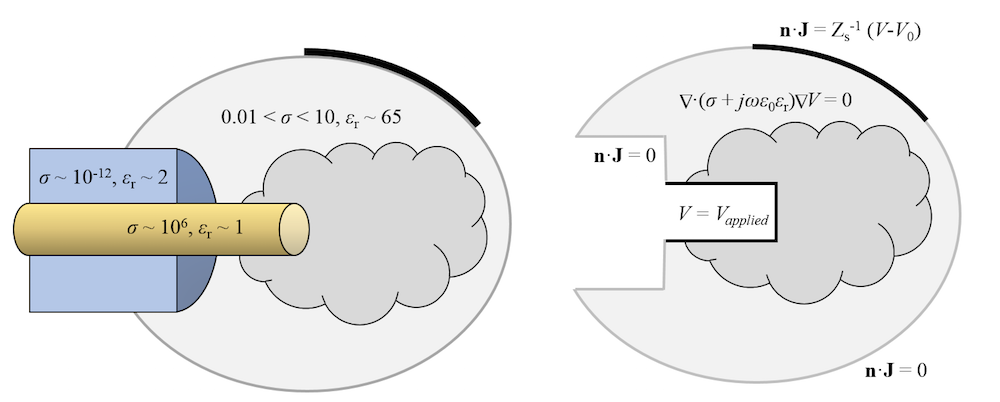
A schematic of an electrical model of radiofrequency tissue ablation. Representative material properties are shown on the left. The modeling domain and governing equations are shown to the right.
Computing Temperature Rise in Human Tissue
The objective of the thermal model is quite straightforward: to compute the rise in tissue temperature over time due to the electrical heating and predict the size of the ablated region. The governing equation for temperature, T, is the Pennes Bioheat equation:
where \rho and C_p are the density and specific heat of the tissue, while \rho_b and C_{p,b} are the density and specific heat of the blood perfusing through the tissue at a rate of \omega_b. T_b is the arterial blood temperature and Q_{met} is the metabolic heat rate of the tissue itself. This equation is implemented within the Heat Transfer Module. If the last two terms are omitted, then the above equation reduces to the standard transient heat transfer equation.
It is also necessary to specify boundary conditions on the exterior of the modeling domain. The most conservative condition would be the Thermal Insulation boundary condition, which implies that the body is perfectly insulated. This would lead to the fastest rise in temperature over time. A more physically realistic boundary condition would be the Convective Heat Flux condition:
with a heat transfer coefficient of h = 5-10 W/m^2K and an external temperature of T_{ext}=20-25 ^{\circ}C. This reasonably approximates the free convective cooling from uncovered skin to ambient conditions.
Along with the change in temperature, we also want to compute the tissue damage. The Heat Transfer Module offers two different methods for evaluating this:
- Time-at-temperature threshold analysis: If the tissue is heated above a specified damage temperature for a specified time (e.g., over 50°C for over 50 seconds) or if a peak temperature of necrosis is ever instantaneously exceeded (e.g., 100°C), then the tissue is considered irreversibly damaged. A tissue damage fraction is also computed based upon the damage temperature and time (e.g., over 50°C for 25 seconds would lead to 50% damage).
- Energy absorption analysis: Given a frequency factor and activation energy that are properties of the tissue being studied, the Arrhenius equation is used to compute the fraction of damaged tissue.
Along with these predefined damage integrals, it is also possible to implement a user-defined equation for damage analysis via the equation-based modeling capabilities of COMSOL Multiphysics.
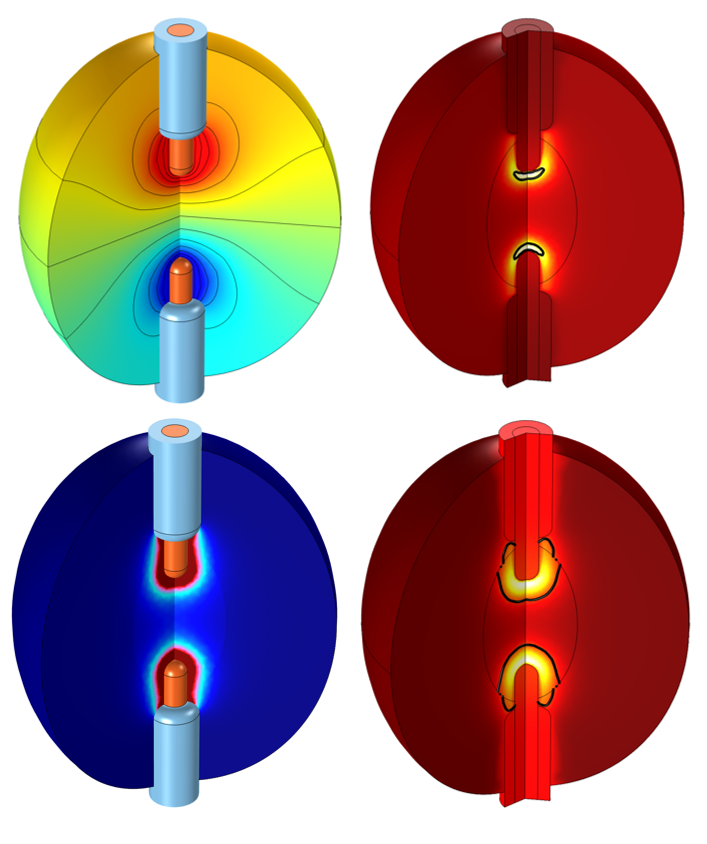
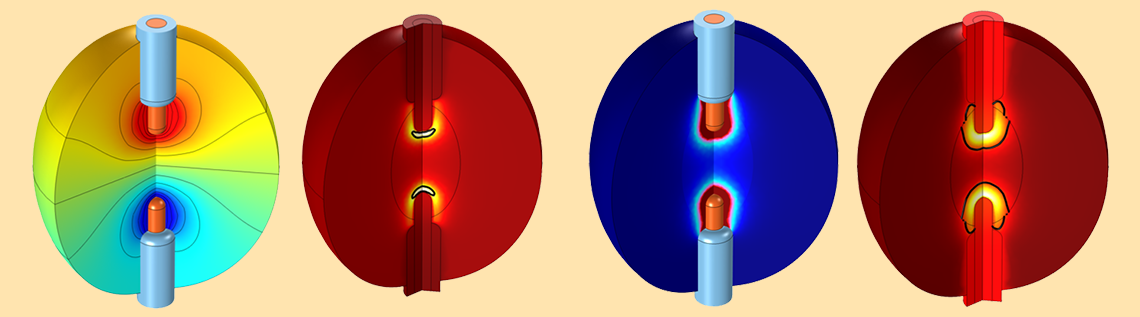
Representative radiofrequency ablation results from a 2D axisymmetric model. Two insulated applicators are inserted into a tumor within the body to heat and kill the diseased tissue. The plotted results include the voltage field (top left), resistive heating (bottom left), and the temperature and size of the completely damaged tissue at two different times (right).
Solving the Coupled Problem to Understand Radiofrequency Tissue Ablation
We have now developed a model that is a combination of a frequency-domain electromagnetics problem and a transient thermal problem. COMSOL Multiphysics solves this coupled problem using a so-called frequency-transient study type. The frequency-domain problem is a linear stationary equation, since it is reasonable to assume that the electrical properties are linear with respect to electric field strength over one period of oscillation. Thus, COMSOL Multiphysics first solves for the voltage field using a stationary solver and then computes the resistive heating. This resistive heating term is then passed over to the transient thermal problem, which is solved with a time-dependent solver. This solver computes the change in temperature over time.
The frequency-transient study type automatically accounts for material properties that change with temperature and the tissue damage fraction. If the temperature rises or tissue damage causes the material properties to change sufficiently to alter the magnitude of the resistive heating, then the electrical problem is automatically recomputed with updated material properties. This can also be described as a segregated approach to solving a multiphysics problem.
In such thermal ablation processes, it is also common to vary the magnitude of the applied electrical heating to pulse the load on and off at known times. In such situations, the Explicit Events interface can be used, as described in our earlier blog post on modeling periodic heat loads. If you instead want to model the heat load changing as a function of the solution itself, then the Implicit Events interface can be used to implement feedback, as described in our earlier blog post on implementing a thermostatic controller.
Explore More Resources for Radiofrequency Tissue Ablation Modeling
If you are interested in studying radiofrequency tissue ablation, there are several other resources worth exploring. If your electrodes have sharp edges and you are concerned about localized heating near these edges, consider adding fillets to your model, since a sharp edge leads to a locally inaccurate result for the heating. Also keep in mind that, despite any locally inaccurate heating, the total global heating will nevertheless be quite accurate with a sharp edge. Thus, the filleting of sharp edges is not always necessary, since the local temperature field can still be quite accurate.
If there are any relatively thin layers of materials that have relatively higher or lower electrical conductivity compared to their surroundings, consider using the Electric Shielding or Contact Impedance boundary conditions for the electrical problem. There are similar boundary conditions available for thin layers in thermal models as well.
If you are interested in modeling at much higher frequencies, such as in the microwave regime, then you need to consider an electromagnetic wave propagating through the tissue. In such cases, look to the RF Module and the Conical Dielectric Probe for Skin Cancer Diagnosis example in the Application Gallery. At even higher frequencies in the optical regime, a range of modeling approaches are possible, as described in our blog post on modeling laser-material interactions.
The heat source for your problem need not even be electrical. High-intensity focused ultrasound is another ablation technique and can be modeled, as described in the Focused Ultrasound Induced Heating in Tissue Phantom tutorial in the Application Gallery.
In closing, we have shown that COMSOL Multiphysics, in conjunction with the AC/DC Module and Heat Transfer Module, gives you the capability and flexibility to model radiofrequency tissue ablation procedures.
If you are interested in using COMSOL Multiphysics for this type of modeling, or have any other questions, please contact us.



Comments (8)
Alexander Warning
January 21, 2016In the heat source term, Q = 1/2 J dot E. Is the 1/2 due to time averaging the cycles? When is there a 1/2 or just 1 in front such as Q = sigma * E^2?
Thank you for this blog
Walter Frei
January 21, 2016 COMSOL EmployeeYes, the 1/2 term is due to the cycle-averaging.
Best Regards,
Sundeep Singh
February 2, 2016How can i incoorporate arrhenius equation for two compartment model in which tumor is surronded by a tissue. When using two biological tissues and entering different arrhenius parameters, i get an error that duplicate parameters created.
Bridget Cunningham
February 3, 2016 COMSOL EmployeeHello Sundeep,
Thank you for your comment.
For questions specific to your modeling work, please contact our support team.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Bram Kraeima
November 8, 2017Hello,
How do I plot the damaged tissue?
Kind regards,
Bram Kraeima
Caty Fairclough
December 1, 2017Hi Bram,
Thanks for your comment.
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Adriona Kelly
August 6, 2021Hi Walter
How was the following heat transfer coefficient value of 5-10W/m^2.K determined? is their a reference for this?
Kind regards
Adriona
Central BioHub GmbH
October 15, 2022Human tissue banking for research is critical to unlocking the next level of discoveries. A detailed study of banked tissue samples separated from human donors allows for a more in-depth analysis of the biological processes involved in disease occurrence and progression.
https://centralbiohub.de/biospecimens/tissue-bank