Guest blogger Junghwan Kook of Jabra introduces a multiphysics topology optimization framework, goes over its advantages, and demonstrates how to use it. This guest blogger is the author of the paper listed as Ref. 1, and the blog post uses some of the same illustrations.
This blog post introduces a multiphysics topology optimization framework with the COMSOL Application Programming Interface (API) and LiveLink™ for MATLAB®, published in Structural and Multidisciplinary Optimization, (Ref. 1). The framework is demonstrated with an acoustic–structure interaction (ASI) problem, which can be solved using the COMSOL Desktop®. The strength of the framework is that it enables you to solve problems that are (currently) incompatible with the COMSOL Desktop®.
Motivation
Topology optimization problems are always solved with gradient-based methods, which require the use of adjoint sensitivity analysis. The COMSOL Desktop® supports solving such problems if the underlying equation is stationary or transient. The most common problems, including frequency-domain problems, are thus fully supported. As for the abovementioned framework, it offers some unique advantages in certain situations. For instance, it enables you to:
- Combine objectives or constraints with stationary and transient solvers
- Test custom optimization solvers
- Utilize support for inconsistent sensitivities, including sensitivity filtering or similar heuristics
- Change the value of numerical parameters between iterations without reinitializing the optimization solver
While these advantages may be most relevant to users working in an academic settings, there are some advantages that will appeal to all users. For instance, the framework can avoid redundant computation in the following situations:
- For problems with sweeps (such as multiple load cases), you can avoid computing the sensitivity of constraints for all values of the sweep parameter
- For cases where a sweep parameter only affects some dependent variables, it is possible to limit the solution to those variables for all but the first value of the sweep parameter
Avoiding some of this redundant computational work may be less important in the context of iterative solvers, and one should keep in mind that the presented framework adds both computational and engineering time. Nevertheless, the framework does have the potential to provide speedup for the listed situations.
Topology Optimization
A topology optimization framework can be implemented by utilizing the capabilities of LiveLink™ for MATLAB®, which allows us to leverage the power of the COMSOL Multiphysics® software while taking advantage of the ease of use and fast implementation in the MATLAB® programming environment.
Topology optimization is an effective approach to optimizing material distribution within a given design space for a given load and boundary condition while meeting the product’s performance goals. Using the topology optimization method in the early concept design phase saves time by replacing expensive and cumbersome design iterations to achieve the best possible design results. Despite the continued development and widespread adoption of topology optimization over the past few decades, applying topology optimization to new application domains (i.e., combining topology optimization with physical processes not natively supported by existing software packages) remains challenging. A few difficulties of developing a multiphysics topology optimization algorithm or program are listed below:
- Developing finite element models for multiphysics problems
- Material interpolation and parameterization of design variables
- Objective function and design sensitivity analysis
- Postprocessing and manipulating the resulting topology design
The challenges listed here often make the average practitioner and researcher hesitant to extend published educational examples and simple frameworks to their multiphysics topology optimization.
The topology optimization algorithm and program discussed here are developed with the COMSOL API and LiveLink™ for MATLAB® for those who want to use the topology optimization design in their multiphysics problems.
Development of Finite Element Models for Multiphysics Problems
We can access and easily manipulate all the features and data structures of COMSOL® models through the COMSOL API using model objects, which provides several methods that let users perform tasks such as creating geometry and meshes and setting up and running sequences of operations to solve models. The structure of the model object complies with the Java® programming language environment and provides several methods for performing the set of tasks required for finite element analysis and optimization. We can use LiveLink™ for MATLAB® to access model objects and utility functions.
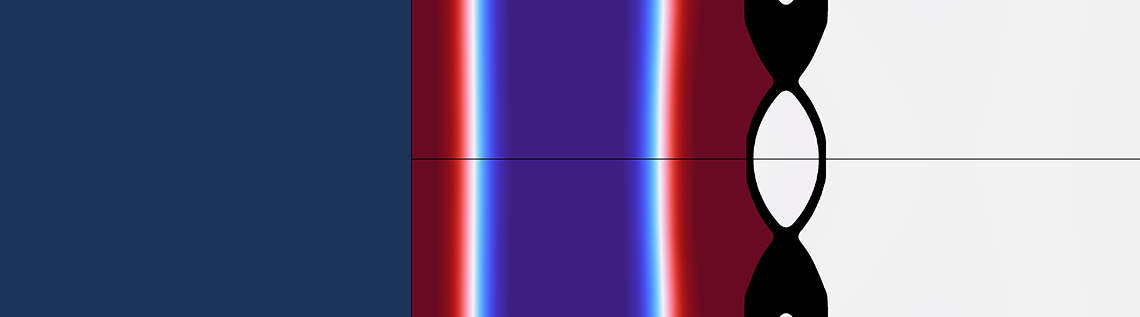
Topology optimization of ASI problems is employed to demonstrate the effectiveness of the introduced framework for systematically designing multiphysics problems (Ref. 1). The design problem of a partition structure between two acoustic domains is shown in Figure 1, which has been used as a benchmark problem in several topology optimization problems that account for ASI problems. You can use topology optimization to design the partition structure so that the acoustic pressure radiated from the inlet is minimized at the outlet.
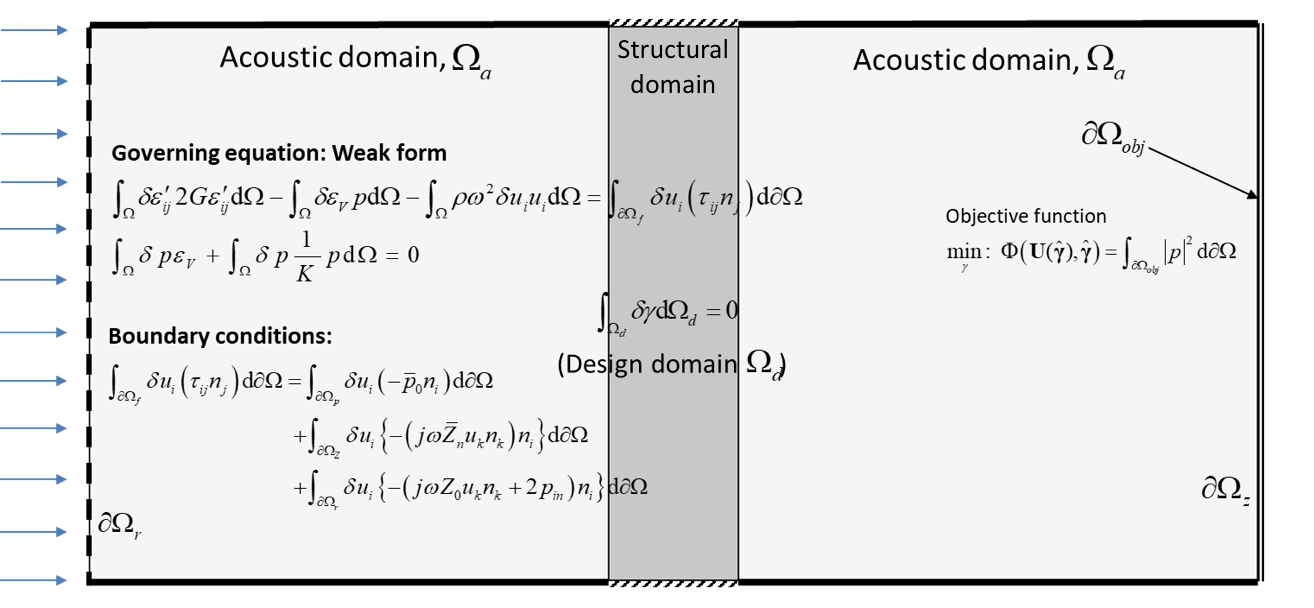
Figure 1. Schematic illustration of a benchmark topology optimization problem accounting for acoustic–structure interaction.
In the example, the mixed finite element formulation using displacement (\textbf{u}) and pressure (p) as state variables (a \textbf{u}/p formulation) is employed to solve the topology optimization problem of the ASI problems. We can model all structural, acoustic, and fully coupled ASI problems without explicitly constructing boundary conditions between acoustic and structural domains by changing the material properties in the mixed \textbf{u}/p formulation. The mixed \textbf{u}/p formulation therefore facilitates density-based topology optimization for structure–acoustic interaction problems.
The mixed finite element formulation is supported by COMSOL®, but the framework is not limited to the software’s physics interfaces, as it includes equation-based modeling functionality from the MATLAB® programming environment. As seen in Figure 2, for instance, the domain integral term for the displacement field presented in Figure 1 expands to the intuitive weak form (see Eq. (A)), and you can easily implement the equation with COMSOL-interpretable syntax using the Weak Form PDE interface as
-((test(ux)-test(vy))*G*(ux-vy)+(test(uy)+test(vx))*G*(uy+vx))
+(test(ux)*p+test(vy)*p)+rho*omega^2*(test(u)*u+test(v)*rho*v.
For further details on implementing the weak form in the COMSOL API, see References 2 and 3. Furthermore, you could get some inspiration for implementation by looking at the lines of code shown in Figure 3, which indicate essential steps for a topology optimization framework. For instance, Eq. (A), (B), and (C) in Figure 2 can be implemented by using the model object and methods shown in Figure 3.

Figure 2. The weak form equations for the acoustic–structure interaction problems using the mixed \textbf{u}/p formulation and some essential tasks needed for topology optimization problems. Finite element system equations including design variables and state variables, e.g., Eq. (E); objective function and constraint, e.g., Eq. (F); and design sensitivity analysis, e.g., Eq. (G).
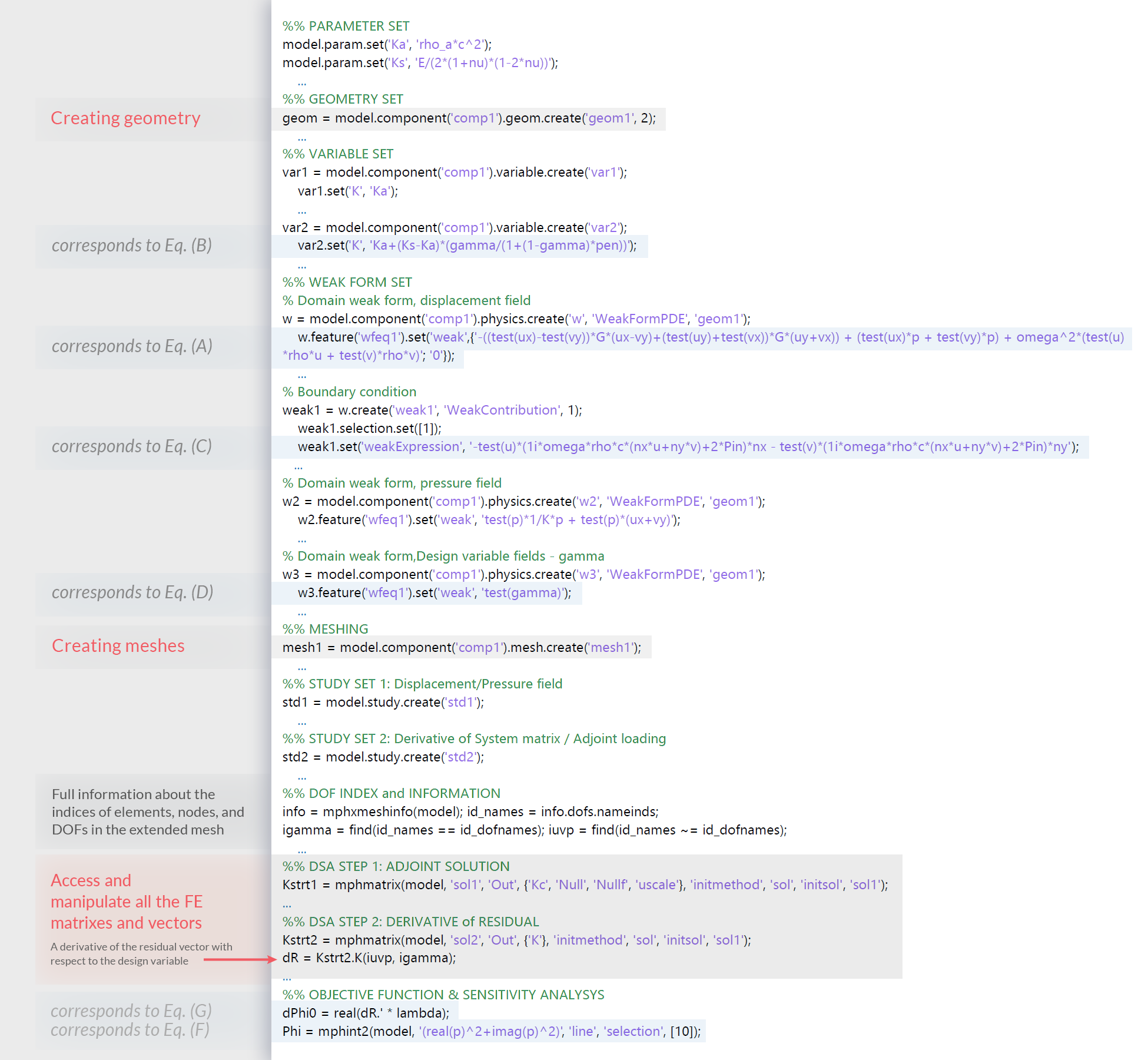
Figure 3. Selected COMSOL API and MATLAB® coding lines for the tasks required for the topology optimization process. The COMSOL API syntaxes can handle required tasks easily and conveniently, without many lines of complex coding.
Material Interpolation and Parameterization of Design Variables
Topology optimization ultimately finds the optimal distribution of one material and other material (or void) in the design domain to optimize the objective function. In the optimization process for the ASI problem, the optimized design is obtained by allowing the density \rho, bulk modulus K, and shear modulus G to take values between the two extreme values corresponding to air and solid materials, which are introduced by the material interpolation function with a design variable field, \gamma, as seen in Eq. (B) in Figure 2.
where p_K and p_G are parameters that can penalize intermediate value of the design variable field. Using equation-based modeling in COMSOL Multiphysics, we can easily introduce the design variable field as an auxiliary dependent variable in the model. Therefore, an additional governing equation in the design domain is introduced, as seen in Eq. (D) in Figure 2. In the codes seen in Figure 3, the domain integral term on the design domain is defined by setting test(gamma), where the design variable, gamma, is set in the Weak Form PDE interface as a dependent variable. It should be noted that the Weak Form PDE interface for the design variable is never solved, but is only used to update design variables based on the optimization procedure.
COMSOL® solvers allow us to solve parts of a problem using a decoupled approach while fixing subsets. For example, the subset equation \textbf{S}_\text{U}\textbf{U} = \textbf{L}_\text{U} can be solved for state variable fields while keeping the values of the design variables at their initial values. The values of the design variables are updated in subsequent iteration steps. To access and update the assembled matrix, we utilize the list of degrees of freedom (DOFs) corresponding to the design variable and the state variable, which is extracted using the mphxmeshinfo function. The advantage of this approach is that we use the vectorized operations in MATLAB® without having to use finite element-wise operations, improving both the readability and performance of the code. Since this implementation method does not depend on the optimizer, it can be used with any optimization solver (i.e., any gradient-based or gradient-free optimizers).
Objective Function and Design Sensitivity Analysis
In the example provided here, the objective function in an integral form in Eq. (F) of Figure 2 can be evaluated using the built-in function mphint2 (seen in the lines of code shown in Figure 3).
The adjoint variable method (AVM) is often used in design sensitivity analysis due to its high efficiency in evaluating the design sensitivity of a system involving a large number of design variables. We can easily construct the adjoint equation and derivatives using the mphmatrix function, which extracts desired matrices and vectors and returns them in a MATLAB® structure format. In particular, the derivative term required for design sensitivity analysis seen in Eq. (G) can be extracted directly from the assembled matrix by specifying the indices of the state and design variables since the design variable field is treated as one of the state variables in the assembled matrix. The design sensitivity analysis can be applied to other problems without substantial modifications.
Postprocessing and Manipulating the Resulting Topology Design
LiveLink™ for MATLAB®, which provides an accessible visualization method, produces clear visualizations of the results of optimization analysis at each optimization iteration and the overall operation of the developed program for troubleshooting and fixing the problems that may arise during optimization. Figure 4 shows topology designs at every iteration and the iteration history of the objective function and volume fraction, which are visualized in the MATLAB® environment.
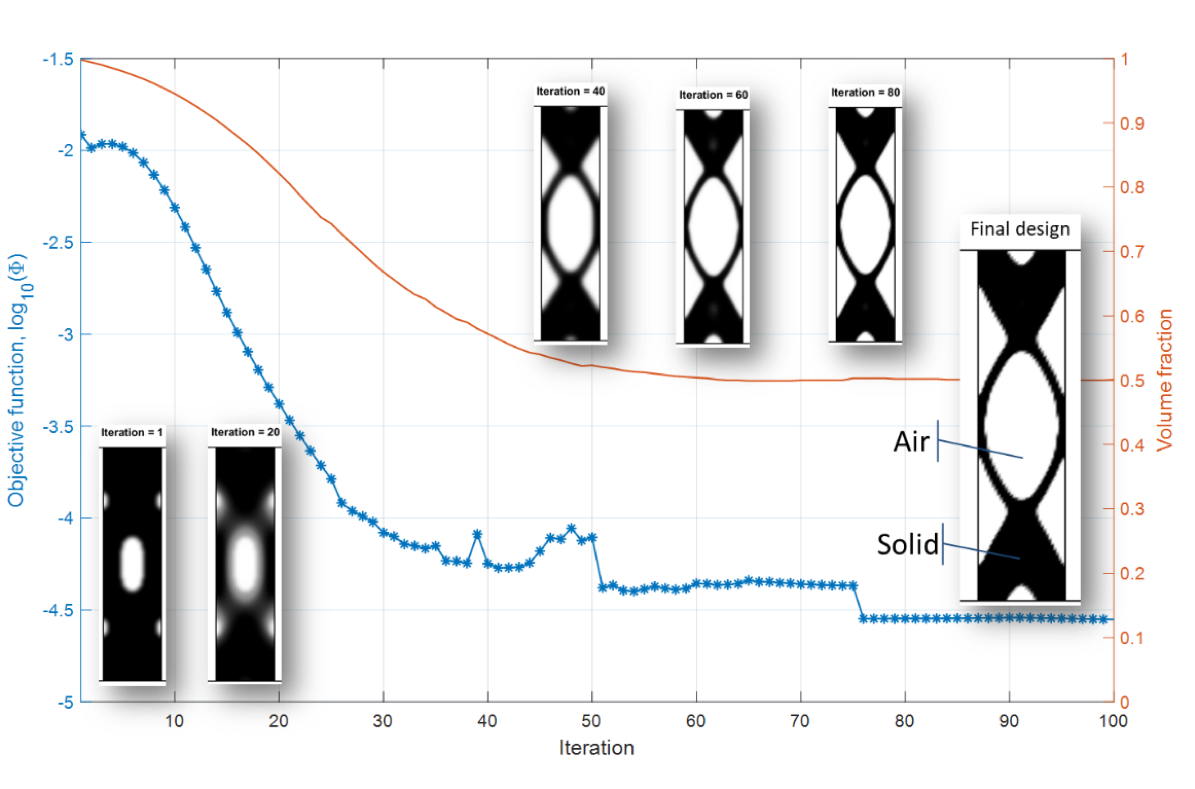
Figure 4. Topology designs (Ref. 1) at every iteration and the iteration history of the objective function and volume fraction are visualized in the MATLAB® environment.
Solving multiphysics problems in a simulation software requires various plots from the topology solutions to interpret the optimization design. We can save the final model developed in the LiveLink™ for MATLAB® environment in an MPH file that contains COMSOL® model objects, including all methods and data structures. The saved solution can be opened in the COMSOL Desktop® environment to postprocess and manipulate the resulting topology in the design workflow. We can then use the Model Builder window to easily create different plots of topological solutions. As seen in Figure 5, the final design with the distinct boundary between the solid and air is obtained through postprocessing using a filter function. A deformed structure is generated to illustrate the operational deflection shape of the optimized topology design in order to show the performance.
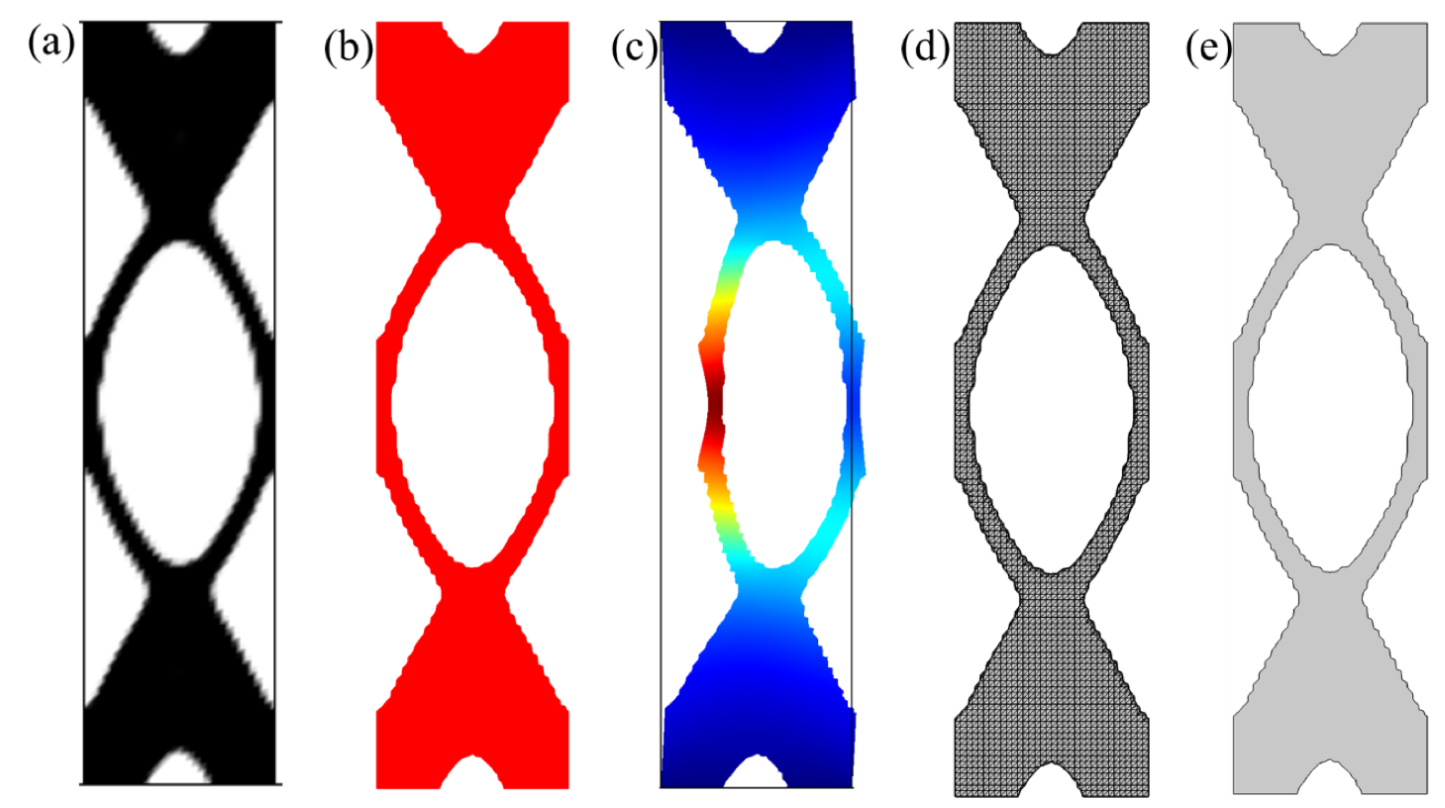
Figure 5. (a) Final design obtained after the optimization. (b) The resulting topology with the clear coupling boundaries using the threshold filtering. (c) The deformed structure with the displacement magnitude field. (d) Imported mesh part. (e) The 2D geometry created by the imported mesh part for 3D printing and additive manufacturing. All figures are taken from Ref. 1.
Optimized designs can be exported as CAD models for further analysis and prototyping. With the data set imported into COMSOL Desktop®, we can create mesh files and CAD files with the optimization results. The geometry objects can be used for further analysis or they can be exported for 3D printing.
Reproduce the Topology Optimization Problem Using COMSOL Desktop®
This blog post provides insight into multiphysics topology optimization using the COMSOL API and LiveLink™ for MATLAB®, as well as an overview of other related topics, including finite element and design sensitivity analysis as well as postprocessing. The COMSOL API and LiveLink™ for MATLAB® enable beginners to enter the field of topology optimization at an advanced level with minimal coding effort. The generalized framework covered in this blog post enables us to solve other types of topology optimization problems without substantial modifications since the methods of discretization and sensitivity analysis of design variable fields are not limited to specific problems. Furthermore, the introduced framework provides the same level of development freedom as high-level languages, which does not limit us to studying new topology optimization techniques and methodologies that require access to optimization parameters and some matrices and vectors in numerical computations. It also provides an efficient way to troubleshoot and fix problems that may arise during optimization.
Note: To get a comprehensive description and code for carrying out the optimization using LiveLink™ for MATLAB®, check out Ref. 1.
In addition, COMSOL Multiphysics offers the user-friendly Optimization Module add-on, which enables you to solve topology optimization problems through its multiphysics and user-defined partial differential equation solvers. Using COMSOL Desktop® for topology optimization, we can reproduce the same multiphysics topology optimization problem using only the built-in functionality (see Figure 6). The model uses the mixed formulation option for Solid Mechanics (for the optimization domain) and Pressure Acoustics (for the pure acoustic domains), combining with the latest optimization method and filtering schemes in the Optimization Module.
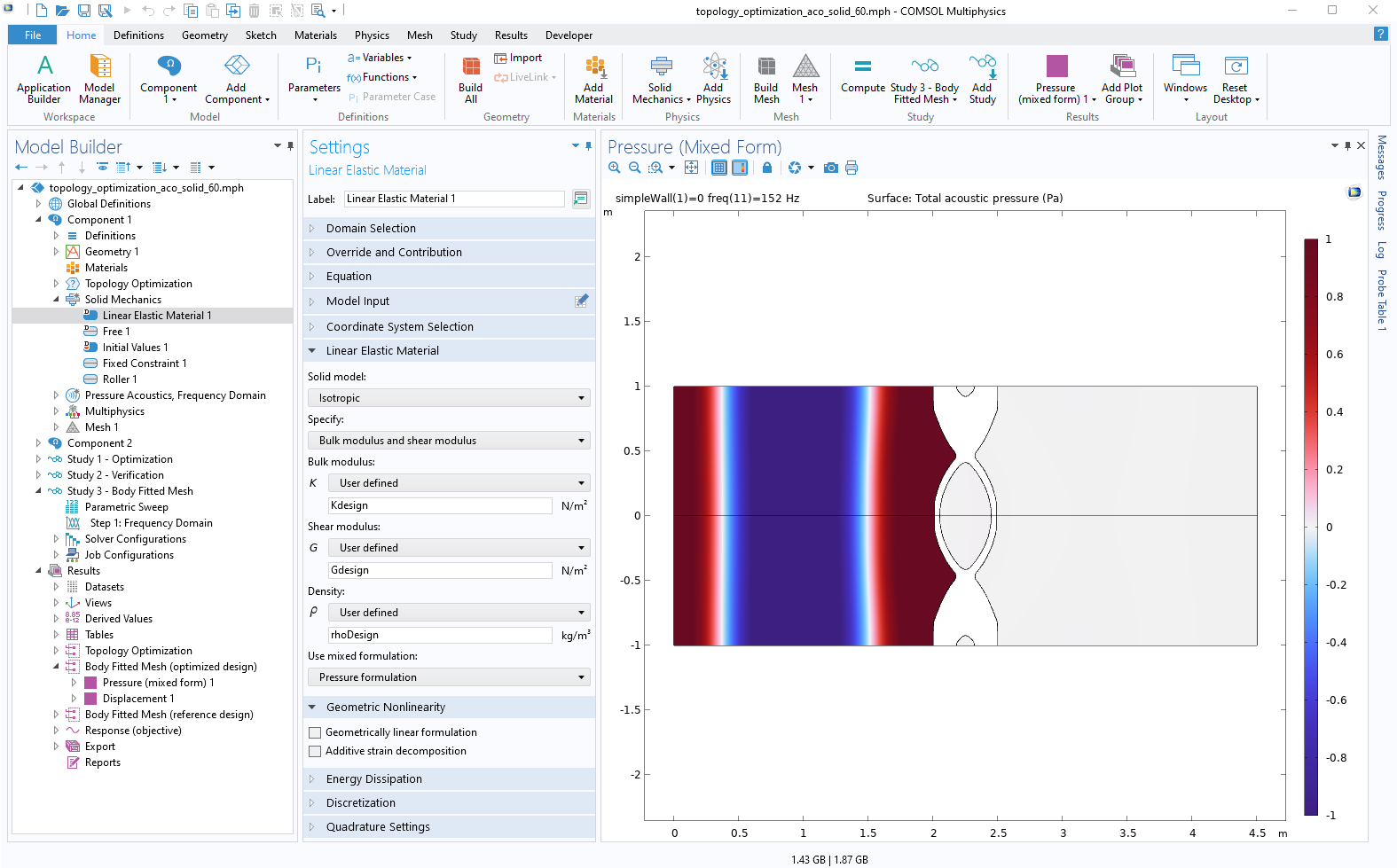
Figure 6. Reproducing the same multiphysics topology optimization problem using only the built-in COMSOL Desktop® functionality.
You can check out the model, shown in Figure 6, by clicking the button below, which will take you to the Application Gallery entry.
About the Author
Junghwan Kook (JK) received his PhD from the School of Information and Mechatronics, Gwangju Institute of Science and Technology, South Korea (2012). As a postdoctoral researcher, JK continued his research at the Department of Mechanical Engineering, Technical University of Denmark (DTU). He was an assistant professor at the Center for Acoustic Micro Mechanical System in the Department of Electrical Engineering, DTU (2015–2017). Since 2017, JK has been a research scientist at the Audio Research, GN Audio A/S, (known as Jabra, a leading brand in engineering communications and sound solutions — innovating to empower both consumers and businesses). His current research interests include multidisciplinary design optimization, numerical methods for acoustic and mechanical designs, sound quality, and experimental analysis of acoustic and vibroacoustic properties. JK has been consistently inspired by modeling and simulating real-world multiphysics systems to deliver high-quality solutions using COMSOL Multiphysics.
References
- J. Kook and J.H. Chang, “A high-level programming language implementation of topology optimization applied to the acoustic-structure interaction problem,” Structural and Multidisciplinary Optimization, vol. 64, pp. 4387–4408, 2021.
- C. Liu, “Implementing the Weak Form in COMSOL Multiphysics,” COMSOL Blog, 2015; https://www.comsol.com/blogs/implementing-the-weak-form-in-comsol-multiphysics
- C. Liu, “Implementing the Weak Form with a COMSOL App,” COMSOL Blog, 2015; https://www.comsol.com/blogs/implementing-the-weak-form-with-a-comsol-app
MATLAB is a registered trademark of The MathWorks, Inc. Oracle and Java are registered trademarks of Oracle and/or its affiliates.



Comments (0)