Optimization Blog Posts

Finding a Structure’s Best Design with Topology Optimization
Think about the first architects who designed a bridge above water. The design process likely included several trials and subsequent failures before they could safely allow people to cross the river. COMSOL Multiphysics and the Optimization Module would have helped make this process much simpler, if they had computers at the time, of course. Before we start to discuss building and optimizing bridges, let’s first identify the best design for a simple beam with the help of topology optimization.
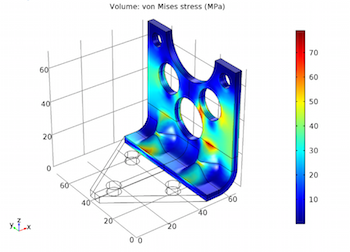
Multistudy Structural Optimization of a Bracket
Weight reduction is a key focus in the automotive industry, where lightweight materials equal more fuel-efficient cars. Here, we perform a multistudy structural optimization of 1 component.

Student Team Wins R&D Award for Optimizing a Mini Race Car
The winning team of the 2014 Formula 1 in schools competition, an international student car building challenge, used COMSOL Multiphysics® to optimize the topology of their car’s wheels.

Fitting Measured Data to Different Hyperelastic Material Models
Want to fit your experimental data to different hyperelastic material models? You can with the Optimization interface in COMSOL Multiphysics®, which lets you fit a curve to multiple datasets.

New Book on Topology Optimization for Electromagnetics
Whether you’re a student or an industry engineer, read Multiphysics Simulation: Electromechanical System Applications and Optimization, a reference guide on simulation and topology optimization.
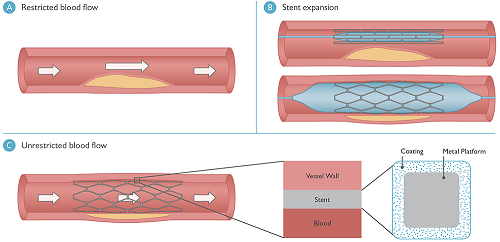
Understanding Drug-Eluting Stents at Boston Scientific
Stents open plaque-blocked arteries, but when an excessive amount of tissue grows over a bare metal arterial stent, it can cause the artery to narrow again in a process called restenosis.

Optimizing Heater Power for Thermal Processing
We demonstrate a useful approach for process control modeling and optimization using COMSOL Multiphysics® and the Optimization Module.
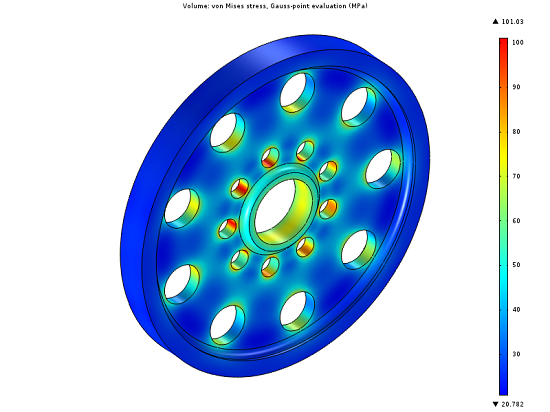
Using Gradient-Free Optimization
The COMSOL Optimization Module includes both gradient-based and gradient-free optimization techniques. Whereas the gradient-based optimization method can compute an exact analytic derivative of an objective function and any associated constraint functions, it does require these functions to be smooth and differentiable. In this blog post, we examine the use of the gradient-free optimizer, which can consider objective function and constraints that are not differentiable or smooth. The dimensions of a spinning wheel are optimized to reduce the mass while maintaining […]
