General Blog Posts

Probing Your Simulation Results
For a transient simulation, imagine if you could simply insert a virtual sensor in a model at a certain location and then monitor the evolution of a field value over time while solving. In COMSOL Multiphysics® you can do just that by using Probes. You define a probe in the Model Builder tree right under the Model Definitions node. Measuring the value at a point is not the only thing you can do with probes, but in this blog post we […]
What Is COMSOL Multiphysics?
You may be wondering “What is COMSOL Multiphysics?” In short, COMSOL Multiphysics is a comprehensive simulation software environment for a wide array of applications, but structured and user-friendly for all to use. The best way to answer the question of what our software can do is to show you. This is why we have created a video that gives you a brief overview of the capabilities you can possess with the software in your hands.

Introduction to COMSOL Multiphysics, a Book to Get you Started
What does it take to get started using COMSOL Multiphysics? Of course, it depends on where you set the bar. However, grasping the workflow and handling the basic tools can be relatively easy to pick up. To make this process even smoother, first-time users will benefit from the recent major update of the COMSOL Multiphysics instruction manual. The book, Introduction to COMSOL Multiphysics, is a valuable tool for learning COMSOL simulation software and the new version is now available for […]

Metamaterials Make Physics Seem Like Magic
Metamaterials are a new and emerging technology with vast potential to reshape our views on what is and isn’t possible in this physical world of ours. Unlocking the mysteries and overcoming the obstacles associated with metamaterials would lead to a host of technological advances once thought impossible by even the most imaginative of individuals. From making computer chips smaller and faster than the most advanced current ones, to protecting structures from earthquakes, to developing imaging technology that doesn’t harm tissue […]
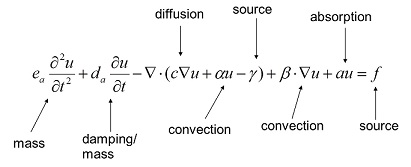
Multiphysics versus FEA
In a popular post from last year, I discussed accessing and manipulating the underlying equations in COMSOL. This blog post instigated reader comments, and most of the respondents appreciated, or even required, the ability to look at the mathematical model (i.e., equations) behind the physics. While considering this, I realized that there is more to the story, and with a little perspective, the community could benefit from further discussion.
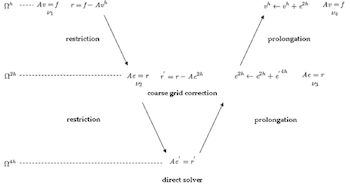
On Solvers: The V-Cycle Multigrid
As discussed previously on the blog, iterative methods efficiently eliminate oscillatory error components while leaving the smooth ones almost untouched (smoothing property). Multigrid methods, in particular, use the smoothing property, nested iteration, and residual correction to optimize convergence. Before putting all of the pieces of this proverbial puzzle together, we need to introduce residual correction and dive a bit deeper into nested iteration. Let’s begin with the latter of these elements.
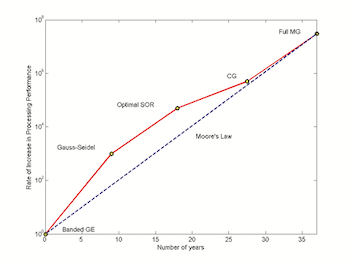
On Solvers: Multigrid Methods
Solution methods are a valuable tool for ensuring the efficiency of a design as well as reducing the overall number of prototypes that are needed. In today’s blog post, we introduce you to a particular type of method known as multigrid methods and explore the ideas behind their use in COMSOL Multiphysics.
Equations: Who Needs Them?
Most of us take mathematical modeling for granted. After all, we’re taught physics and calculus almost hand-in-hand. But we owe a lot to the early pioneers like Isaac Newton, who demonstrated and strongly promoted interpreting natural phenomena through equations. Differential equations are especially useful since most things change as time marches on. Since we live in 3D space, partial differential equations (i.e., equations that express change in more than one “direction”) arise as the prominent tool to express continuum level […]
