Learning Quantum Mechanics Concepts with Double-Barrier Structures

“I think I can safely say that nobody understands quantum mechanics.” — Richard Feynman, in The Character of Physical Law (1965).

Although the Nobel-prize-winning physicist might have been speaking in jest, quantum mechanics is a difficult concept to teach — and simulate. Modeling a double-barrier structure in the COMSOL Multiphysics® software can help teach quantum mechanics concepts to physics students as well as enhance the research and development of semiconductor devices.

What Is a Double-Barrier Structure?

A double barrier is a type of resonant tunneling structure that consists of a quantum well surrounded by very thin barriers that separate the layers.

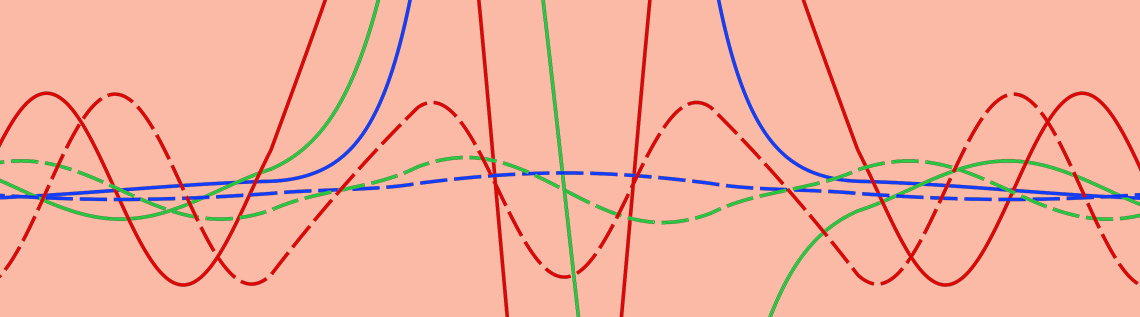
Resonant tunneling in a double-barrier structure.

The structure for a double barrier is simple, so it is often used to demonstrate the concepts of tunneling and quasibound states to physics students learning quantum mechanics. Double-barrier structures are commonly found in resonant tunneling diodes (RTDs) and other semiconductor devices. Therefore, the ability to model these structures is important in the design of semiconductor applications. In this blog post, we discuss a simple example of a double-barrier structure model that can be used for these two purposes.

A tunnel diode, which is a semiconductor component with a working principle based on quantum mechanical tunneling. Image in the public domain, via Wikimedia Commons.

Modeling a Double-Barrier Structure in COMSOL Multiphysics®

In semiconductor and quantum mechanics studies, double-barrier structures are preferable to model because they can be simple and general while staying relevant to semiconductor physics. For this example, we use a 1D model and assume that the structure is constructed from layers of GaAs and AlGaAs.

There is a new predefined interface in COMSOL Multiphysics version 5.3 — the Schrödinger Equation interface — that can solve the single-particle Schrödinger equation for our model (as well as general quantum mechanics problems in 2D and 3D). The interface, available with the Semiconductor Module, assumes the envelope function approximation to compute the electron wave function and the hole wave function in quantum-confined systems. For layered structures such as the current model, the Schrödinger Equation interface accounts for the discontinuity in the effective mass by implementing the BenDaniel-Duke boundary condition.

Four studies are used to illustrate different aspects of the double-barrier structure:

1. Eigenvalue study that solves the eigenenergies of the quasibound states
2. Time-dependent study that solves the time evolution of one of the quasibound states
3. Eigenvalue study that solves the resonant tunneling condition
4. Stationary study that computes the transmission and reflection coefficients

After running these studies, we can take a look at what the results of the simple double-barrier structure model tell us…

Simulation Results

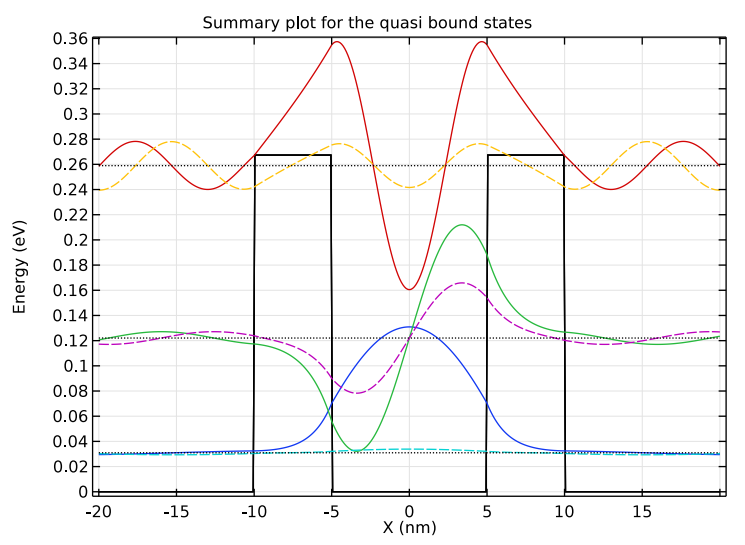
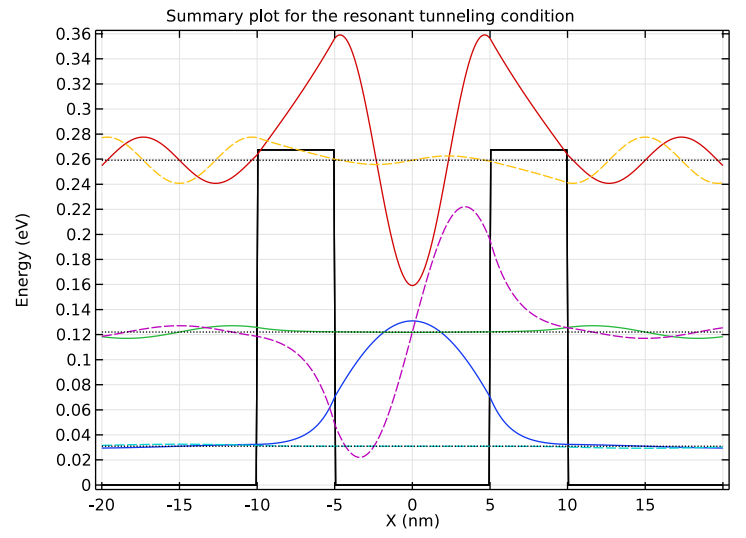
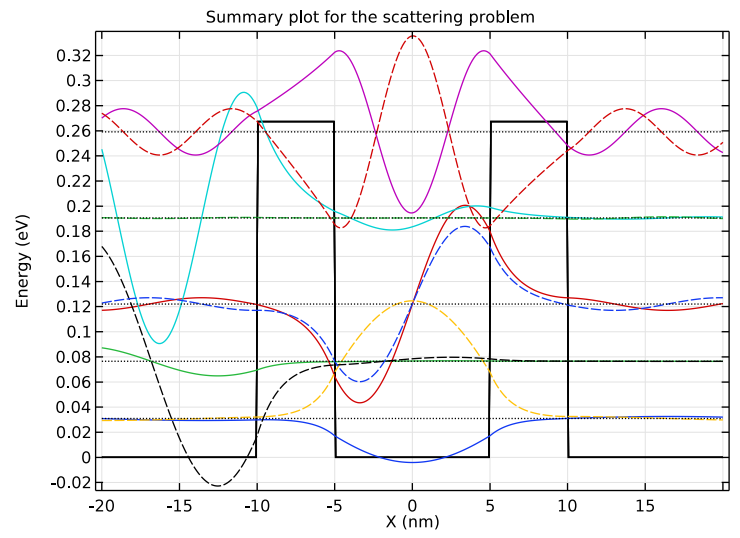
We can plot the simulation results for the different studies in the double-barrier structure model to visualize and compare different values. For example, the results plots help us visualize the eigenenergies for quasibound states, decay of the total probability, resonant tunneling condition, and wave functions for different energies in the double-barrier structure.

Plots showing the quasibound states (left), resonant tunneling condition (center), and scattering problem at different energies (right).

For the time-dependent study, the results show the wave function leaking out of the modeling domain, which can be expected. This behavior is best visualized with an animation, which can be easily generated and exported using the postprocessing features in the COMSOL® software.

By plotting the transmission and reflection coefficients, we can compare them with analytical results to validate the model. All four of the studies generated simulation results that agree well with analytical solutions.

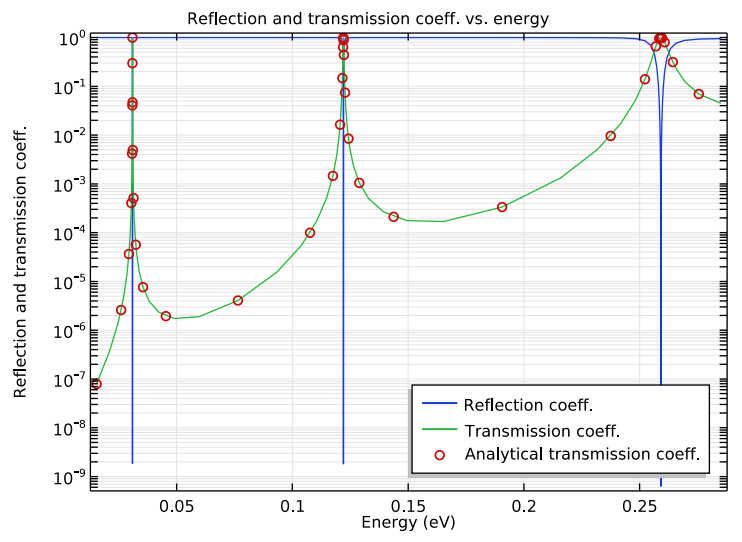
The reflection and transmission coefficients, compared with the analytical results for the transmission coefficient.

The double-barrier structure model is effective for teaching quantum mechanics and simulating practical semiconductor applications. Although Richard Feynman implied that quantum mechanics is a difficult concept to understand, with a simple model, we can analyze semiconductor devices — and pass on the knowledge of these concepts to the next generation of physicists and engineers.

Try It Yourself

Try modeling a 1D double-barrier structure in COMSOL Multiphysics by clicking the button below.

Further Reading

• Learn more about the Schrödinger Equation interface and other updates to the Semiconductor Module
• Read a fun example of quantum mechanics theory and the Schrödinger equation in a previous blog post
• See how to use the Schrödinger Equation interface for creating an app to calculate the band gap in superlattices