Time-Dependent Optimization
Application ID: 12677
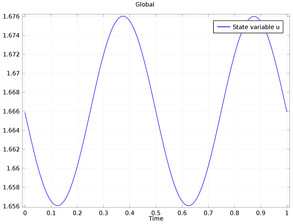
This tutorial demonstrates how to compute the periodic steady-state solution of a nonlinear model problem using an optimization solver. The solver modifies the initial conditions at the beginning of a period to match the solution at the end of the period.
The model solves much faster using this combination of optimization and time dependent solver compared to when using the time dependent solver alone. The reason is that the solution does not have to be computed for a large number of periods in order to reach steady state.
This model example illustrates applications of this type that would nominally be built using the following products:
however, additional products may be required to completely define and model it. Furthermore, this example may also be defined and modeled using components from the following product combinations:
The combination of COMSOL® products required to model your application depends on several factors and may include boundary conditions, material properties, physics interfaces, and part libraries. Particular functionality may be common to several products. To determine the right combination of products for your modeling needs, review the Tabella delle Funzionalità and make use of a free evaluation license. The COMSOL Sales and Support teams are available for answering any questions you may have regarding this.
