High Fidelity TEA Theory Altered Compressible Navier-Stokes CFD Using COMSOL Equation-Based Modeling
It is common knowledge to readers of these COMSOL conference proceedings that COMSOL (as well as other established CFD codes) produces unstable numerical solutions of the Navier-Stokes equations without "consistent stabilization" and/or "inconsistent stabilization" (or similar nomenclature for non-COMSOL codes) enabled.
With aim to replace this approach of added stabilization (perhaps a code option in the future) a novel new theory [1] is summarily presented in this paper denoted "Truncation Error Annihilation" (TEA). The TEA theory provides a new algorithm that mathematically annihilates the algebraic instability mechanism via continuum equation systems alteration with analytically derived Reynolds number dependent cubic nonlinear tensor product calculus functionals. The need for numerical stabilization obviated, tridiagonal stencil equivalent CFD algorithm discretization of theory modified NS/RaNS equations are directly coupled into the unchanged COMSOL "High-Mach Number Flow" equation system following standard procedure for equation-based modeling. Consequently, TEA theory enables an algebraically stable generation of resolutely oscillation-free O(h^4) Taylor-series accurate state variable distribution that is monotone to iteration convergence digit on any discretization.
TEA is applicable to the entire class of NS/RaNS physics, but the choice here is to focus on transonic and supersonic compressible flows. This choice of flow regime is primarily due to the challenge in solving at high-fidelity meshing level, and a requirement of smooth monotonicity, while retaining pure Galerkin interpolation test functionality, with inclusion of accurate shock present flows. Secondarily, both authors have sustained efforts on this issue after the time of primary-author Ph.D. dissertation [2].
The approach is simple for the COMSOL construct. Both consistent and inconsistent stabilization are disabled entirely by "mouse click" in the option box of the code graphical user interface (GUI). Simultaneously, the TEA terms are added through direct option within the COMSOL model tree in weak form as contribution additions for all the state variable equations, written in non-conservative form, on pressure, velocity, temperature, and turbulent eddy viscosity. These equations solve for the conservation of mass, momentum, energy, and turbulent eddy viscosity closure using Spalart-Allmaras turbulence model. TEA theory is presented in non-dimensional form, so the input for solving using COMSOL in both dimensional form on one problem, and non-dimensional form on another problem, are consistently applied to established benchmark cases and demonstrated to yield valid results.
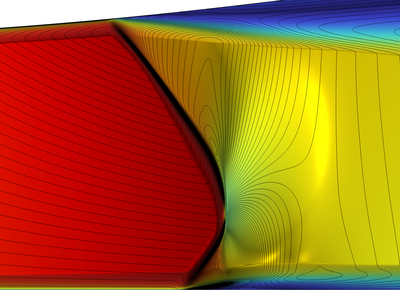
Two classic validation model problems are presented from a subset of the suite of challenge problems in recent AIAA High-Fidelity Workshop Proceedings [3]. The Sajben-diffuser problem is also included in the COMSOL application library. The dimensional form inputs were improved based on NASA references to archival data for geometry and test data. A direct comparison with COMSOL consistent stabilization results is also included for the Sajben-diffuser with all other solution features being equal (mesh, inputs, solver, etc.). Results for a Smooth-Bump long time AIAA challenge problem, defined by non-dimensional input, are also presented. Included is a complete history of COMSOL adaptive mesh procedure, along with classical energy norm convergence data.