Learning Center

Creating a Gaussian Process Surrogate Model from Imported Data

---

To learn how to create a Gaussian Process (GP) surrogate model from imported data with COMSOL^®, we will, for simplicity, use a dataset similar to the example from Part 2 in this article. The data forms a function surface in which the variables , , and can represent any quantity such as displacement, stress, temperature, or current. The workflow presented here is applicable when the data originates from experimental results.

Using a GP model, we can create a smooth surrogate model function and associate uncertainty with the fitted data. Additionally, with the Uncertainty Quantification Module, an add-on to the COMSOL Multiphysics^® software, we can compute statistical metrics such as the global mean and variance of the surrogate model.

Note: The Uncertainty Quantification Module is required for this example.

Fitting Imported Data with Surrogate Models

The data consists of 900 data points and is stored on a text file format with columns for the arguments and function values. The beginning of the text file, available here, appears as follows:

Experimental data in text file format.

We assume that this data represents experimental data. However, in this example we will not be concerned with what the data represents but instead take an abstract approach that is applicable to any type of data. Previously, in Part 2, we learned how to fit experimental data to a linear interpolation function as well as a DNN surrogate model function. Linear interpolation is an efficient method for both 2D and 3D data. However, when creating surrogate models with more than three input arguments, other methods offer significant advantages. Additionally, for noisy data where approximation is needed rather than interpolation, creating a linear interpolation function is often not the best choice. In this article, we will discuss how to use a GP surrogate model to approximate the imported data.

Fitting Imported Data with a Gaussian Process Surrogate Model

Instead of directly importing the data file to a surrogate model function definition, let's start by importing the data file into a table in the software. This makes it easier to reference the same data file from different surrogate models. Start by choosing the Blank Model option in the Model Wizard. Then, under the Results node, right-click the Tables node and select Table.

Adding a table to the results.

In the Table node Settings window, click Import and browse to the text file containing the experimental data. This file contains a header beginning with a % character, which is the standard COMSOL format for comments and headers. The columns will automatically be labeled X, Y, and Z.

The Table node Settings window with the imported data file.

With the Uncertainty Quantification Module, you can now add a Gaussian Process surrogate model function. To do this, right-click Global Definitions, and from the Functions menu select Gaussian Process.

Adding a Gaussian Process surrogate model.

In the Gaussian Process function Settings window, for the Data source choose Results table and select Table 1. The Data Column Settings section will automatically be filled out with default Argument and Function values: x1, x2, and gpm1.

The settings for the GP surrogate model.

In order to assess the uncertainty in the model, we can compute the estimated standard deviation at each point in the dataset. To do this, in the Gaussian Process function Settings window, under the Related Functions section, select Define standard deviation function. This makes a function named gpm1_stddev available, which can be visualized and evaluated just like any other function.

Enabling the standard deviation function, gpm1_stddev, for the GP function, gpm1.

To generate the surrogate model, click Train Model at the top of the Gaussian Process function Settings window. The computation will take a minute or two. Once it is complete, plot the function by clicking the Create Plot button, as shown in the figure below.

The Model Builder with the Function 1 node selected under 2D Plot Group 1 and the corresponding Settings window and Graphics window.

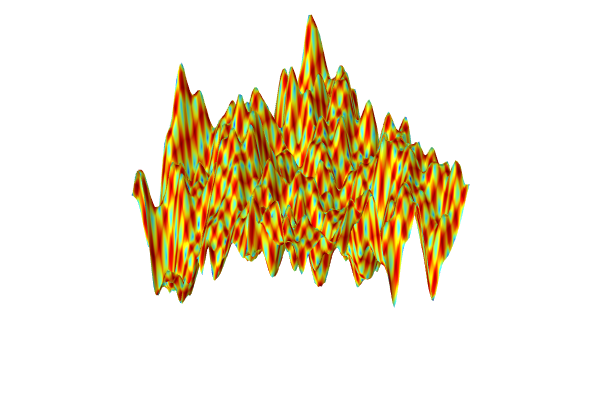
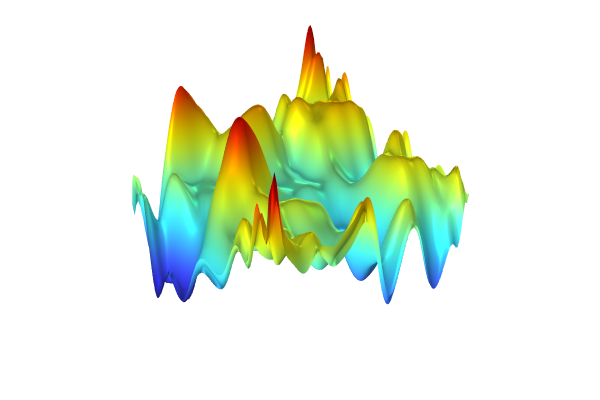
A visualization of the GP surrogate model created from experimental data.

The dataset appears to vary wildly. However, this is due to the automatic z-axis scaling, and upon further inspection, the function values are within a narrow range between about 1.15 and 1.24. We are now interested in computing the pointwise uncertainty in terms of standard deviation as well as the global mean value and standard deviation. Let's start with the pointwise uncertainty. Navigate to the Height data setting under the Height Expression subnode and change it to Expression and type gpm1(x1,x2).

The modified Height Expression subnode settings.

Now, go to the Function node Settings window under the 2D Plot Group node and change the Expression to gpm1_stddev(x1,x2) and click Plot. This generates a visualization of the pointwise standard deviation as a color, as shown in the figure below.

The Model Builder with the Function 1 node selected under 2D Plot Group 1 and the corresponding Settings window and Graphics window.

The standard deviation estimate for the surrogate model.

To better see the uncertainty, we can view the plot in the xy-plane by clicking the xy-button in the Graphics window toolbar. Additionally, click the Orthographic Projection button for a better view without perspective effects. You can also optionally click the Scene Light button to get a more uniform-looking plot.

The Model Builder with the Height Expression 1 node selected and the corresponding Settings window and Graphics window.

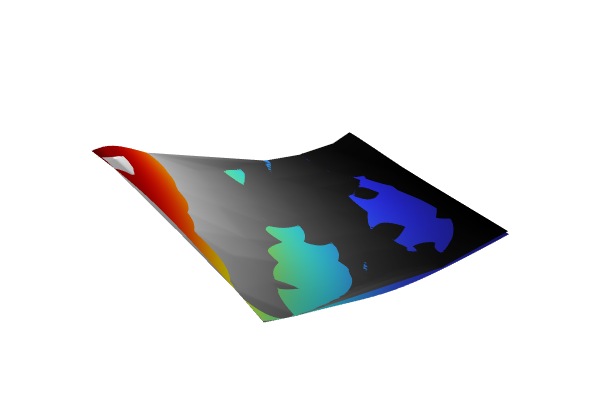
The standard deviation estimate for the surrogate model, viewed in the xy-plane.

From the standard deviation plot, we can see that the data appears to be sampled in a grid since the standard deviation values are near or at zero in the vicinity of the data points.

In general, a few different factors affect the estimated standard deviation values:

• Distance from training points: Points far from the original data points tend to have higher uncertainty because the model has less information to base its predictions on. This includes extrapolated regions.
• Data density: Areas with sparse data points will generally have higher uncertainty.
• Model complexity and noise: The chosen covariance function (kernel) and noise level in the GP model can also affect the uncertainty. More complex models with more noise might show higher uncertainty.

In the Information section, at the bottom of the Gaussian Process function Settings window, you can see the global Estimated error for the surrogate model function fit. This value is scaled relative to the standard deviation of the training data (sample standard deviation). In a case where there are multiple quantities of interest and corresponding functions, there is one estimated error value for each function.

The Information section.

Computing Uncertainty with the Uncertainty Quantification Study

The standard deviation indicates a pointwise error boundary around the predicted values. The pointwise mean function is the surrogate model function itself. The Uncertainty Quantification Module includes a solver option that enables computing the global mean and standard deviation of the surrogate model, alongside with some other statistical quantities. Let's see how to use this solver option, building on the previous example. Right-click the root node in the model tree and select Add Study. Alternatively, in the ribbon, click the Study tab and select Add Study.

Adding a study.

In the Add Study window, select Stationary and then close the Add Study window. Now, right-click Study 1 and select Uncertainty Quantification > Uncertainty Quantification.

Adding an Uncertainty Quantification study.

The Uncertainty Quantification study requires defining quantities of interest and input parameters. Of the five different study type options offered by the Uncertainty Quantification Study, we will select the one called Uncertainty propagation from the UQ study type menu. To learn more about these study types, see our course on uncertainty quantification.

The Uncertainty Quantification study settings with the Uncertainty propagation option selected.

Make sure that you have selected the Uncertainty propagation option. In the Surrogate model settings section, select Gaussian Process 1 for the Gaussian process function.

Selecting an already existing GP surrogate model in the uncertainty propagation study.

Change the Compute action setting from the default Compute and analyze option to the Analyze only option. The Analyze only option will use the already-trained surrogate model function for the analysis. Note that the other settings in the Surrogate model settings section of the Uncertainty Quantification study Settings window only applies when we choose the New option for the Gaussian process function setting.

Selecting Analyze only as the Compute action.

The default surrogate model for uncertainty propagation is Adaptive Gaussian process. However, in this case, we will reuse an existing surrogate model, so the adaptive method will not be invoked. The adaptive method requires the generation of new data points, which is not possible for imported data since there is no finite element model to compute additional data points. Therefore, when we select the Analyze only option, the adaptive method is automatically disengaged, and there is no need to change this setting.

The available surrogate model options are: Adaptive Gaussian process (demonstrated in Part 4), Gaussian process, Adaptive sparse polynomial chaos expansion, and Sparse polynomial chaos expansion, as shown in the figure below. In this example, both the Adaptive Gaussian process and the Gaussian process options use a nonadaptive Gaussian process method.

The Surrogate model option in the Uncertainty Quantification study.

We will need to create two global parameters that will define the input arguments for the already trained surrogate model so that it can be used by the Uncertainty Quantification study. Under Global Definitions > Parameters, create two variables, x1 and x2, as shown in the figure below. The actual values are not going to be used but will be overwritten by the Uncertainty Quantification study.

The two input argument variables for the surrogate model.

In the case of an already trained surrogate model in combination with the Analyze only option, we can use any Expression for the Quantities of Interest. Enter 1 in the Expression field for Quantities of Interest, as shown in the figure below. The imported dataset is defined in the region . The Distribution setting is set to Uniform for both parameters, which is the only option that makes sense in this example, where we would like to analyze a surrogate model that can be used equally well in any part of the parameter space. In the Input Parameters section, add x1 and x2 to the table with a lower bound of 0 and an upper bound of 10 for both parameters.

For an already trained surrogate model combined with the Analyze only option, we can use any expression for the quantities of interest. Enter 1 in the Expression field for Quantities of Interest, as shown in the figure below. The imported dataset is defined in the region . Set the Distribution setting to Uniform for both parameters, which is the only appropriate option in this example, as we want to analyze a surrogate model that can be applied uniformly across the entire parameter space. In the Input Parameters section, add x1 and x2 to the table with a lower bound of 0 and an upper bound of 10 for both parameters.

The settings in the Quantities of Interest and Input Parameters sections.

Now we are ready to analyze the surrogate model. At the top of the Uncertainty Quantification study Settings window, click Compute. Recall that in the case of an Uncertainty Quantification study, the sampled variables are output to a Quantities of Interest table rather than a Design Data table.

When the computation is finished, a kernel density estimation (KDE) plot is shown. The KDE plot is a smoothed histogram plot and represents the probability density function estimate for the function value considering all input values in the region . In other words, the KDE plot shows the most probable function values when the input parameter space is randomly uniformly sampled within the set parameter boundaries.

A KDE plot showing the probability density function estimate for the function values of the imported data.

We can also get statistical information from this computation. If not already visible, select Results > Tables > Uncertainty Propagation > QoI Confidence Interval.

Selecting the QoI Confidence Interval table.

The QoI Confidence Interval table contains information about the surrogate model's global mean and standard deviation as well as minimum, maximum, and various quantile values.

The QoI Confidence Interval table.

The global mean value is computed to about 1.2, and the standard deviation is about 0.014, indicating a near constant dataset. The minimum and maximum values are about 1.15 and 1.24, respectively. Note that these values do not correspond to the original dataset but instead to the fitted surrogate model function.

Using Different Covariance Functions

Let's now briefly consider the influence of covariance functions, or kernels. To illustrate this, we will use a more coarsely sampled dataset with only 25 data points compared to the original 900. The figure below shows an example where we have added a second GP function and changed the covariance setting to the Squared exponential covariance function. This covariance function is smoother than the default Matérn 3/2 option, as it assumes that the sampled data comes from an infinitely differentiable function. For more information on covariance functions, please refer to this article.

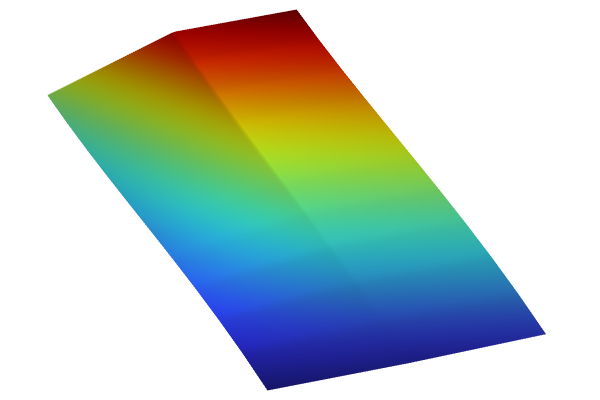
A Gaussian Process surrogate model using a Squared exponential covariance function.

The visualizations below show plots of the surrogate model functions using the Matérn 3/2 and the squared exponential covariance functions. The function based on the Matérn 3/2 option appears slightly more "pointy" than the one using the Squared exponential option. The Matérn 3/2 covariance function assumes that the underlying data is only once differentiable.

Surrogate model functions based on the Matérn 3/2 and Squared exponential covariance functions.

If we compare the pointwise standard deviation of the two functions, we see that the Squared exponential covariance option estimates a lower level of uncertainty. The Matérn 3/2 function provides higher pointwise uncertainty estimates than the Squared exponential function for sparsely sampled datasets because it enables less smooth and more variable functions. This flexibility results in a more cautious model that acknowledges higher uncertainty due to the limited information available, whereas the Squared exponential function, assuming smoother functions, tends to produce lower uncertainty estimates even when data is sparse.

The standard deviation estimates for the Matérn 3/2 and Squared exponential options.

Despite the fact that the Matérn 3/2 covariance function assumes the underlying data is once differentiable, the computed surrogate model function can be smoother. This is because the surrogate model function represents the mean of the GP posterior distribution, which is derived from all possible GP functions that fit the data, given the Matérn 3/2 covariance. In fact, the mean function is a linear combination of Matérn 3/2 covariance functions. For more information, see this resource on covariance functions.