Aggiornamenti Studi e Solutori
Supporto per NVIDIA® GPU
È stato aggiunto il supporto per le GPU per l'acustica di pressione e l'addestramento dei modelli surrogati. Questa funzionalità è disponibile per i sistemi dotati di una GPU NVIDIA® compatibile.
Accelerazione su GPU per l'acustica di pressione tempo-esplicita
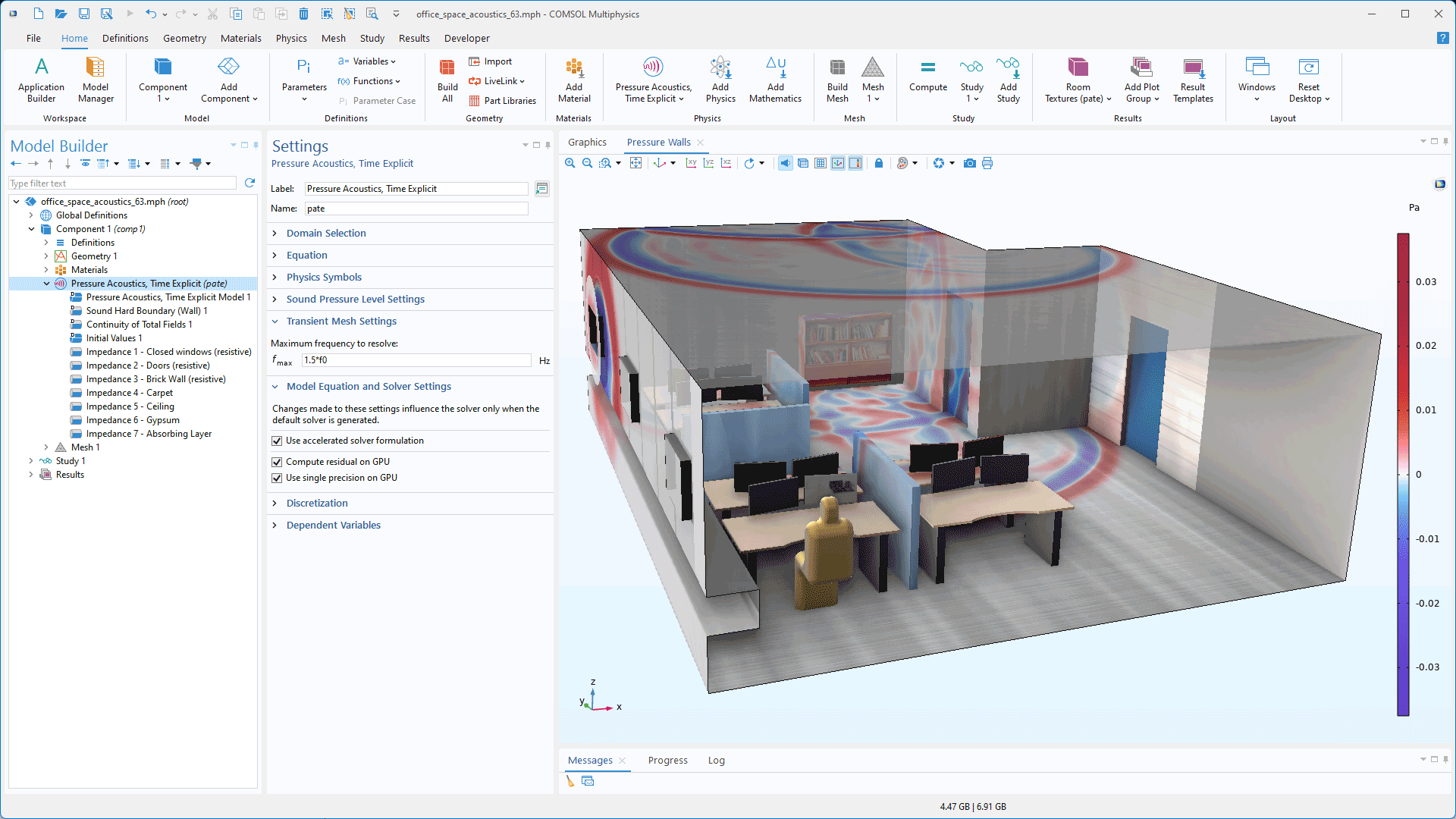
I modelli lineari di acustica della pressione espliciti nel tempo possono ora essere risolti utilizzando una formulazione accelerata che supporta condizioni al contorno di impedenza realistiche. Questa accelerazione può essere notevolmente aumentata quando la formulazione viene utilizzata con una scheda NVIDIA® GPU, anche se l'aumento delle prestazioni dipende dall'hardware. Per abilitare questa funzionalità, è necessario installare un CUDA® Toolkit. (Il percorso del toolkit può essere specificato durante l'installazione). Questa funzionalità è visibile nel tutorial Acoustics of an Open-Plan Office Space. Per maggiori dettagli, si vedano le novità dell'Acoustics Module.
Accelerazione GPU per l'addestramento dei modelli surrogati DNN
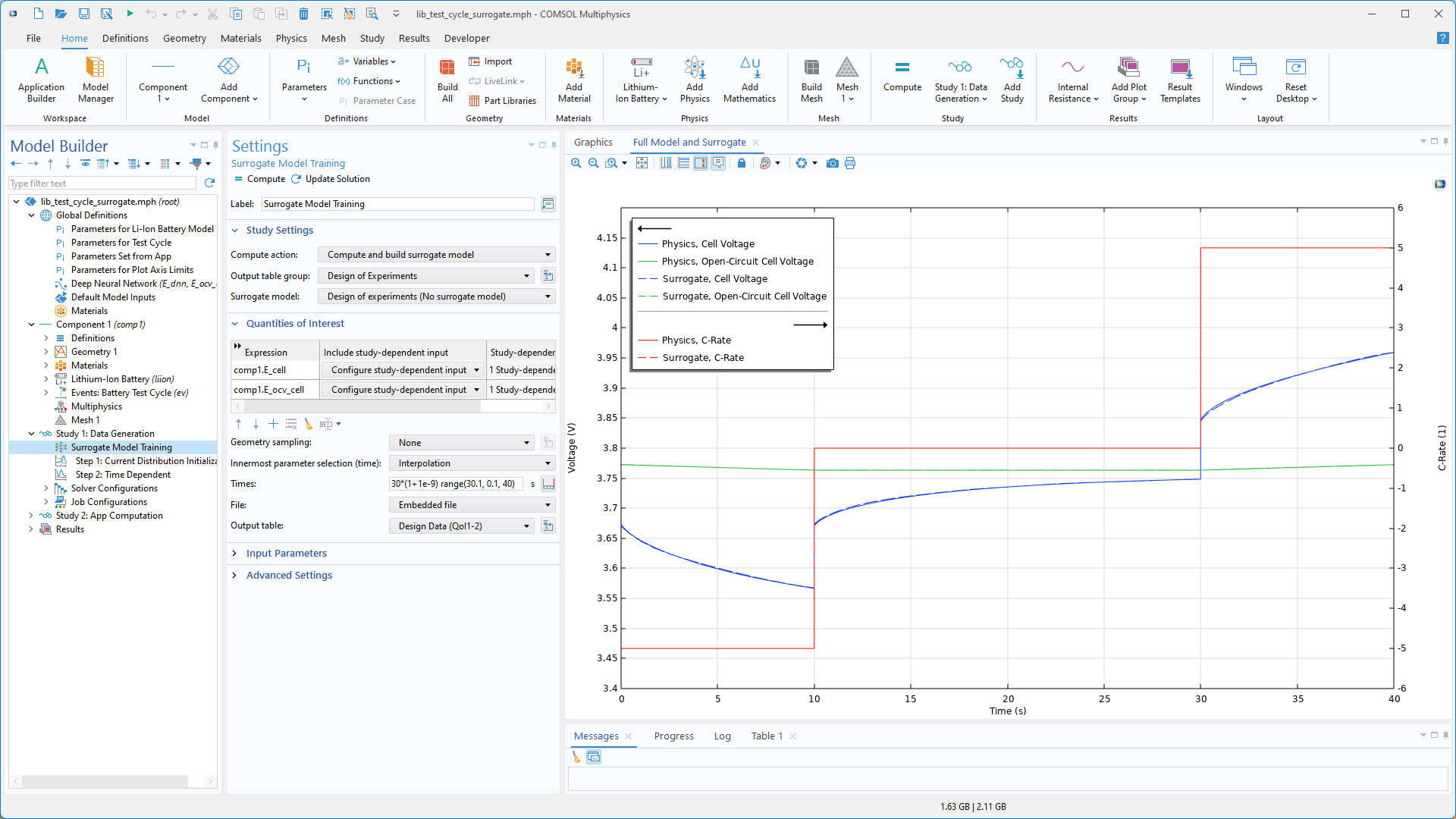
È stato aggiunto il supporto GPU per l'addestramento dei modelli surrogati DNN, accelerando in modo significativo il processo di addestramento e consentendo uno sviluppo più rapido dei modelli surrogati da utilizzare nelle app e in vari contesti di simulazione. Per attivare questa funzionalità, assicurarsi che l'opzione CUDA DNN Support sia selezionata nella pagina Products del COMSOL Installer. Inoltre, è necessario installare il Toolkit NVIDIA® CUDA®, che può essere scaricato dal sito web di NVIDIA®.
Miglioramenti per la generazione dei dati dei modelli surrogati
La generazione di dati dipendenti dallo spazio, dal tempo e dalla frequenza da utilizzare nei modelli surrogati DNN è ora molto più semplice.
L'opzione Geometry Sampling è disponibile nel nuovo sottomenu Surrogate Model Sampling all'interno delle Definitions per i componenti del modello. Questa funzione consente il campionamento dei dati direttamente nei domini, ai contorni, lungo i lati o sui vertici, eliminando la necessità di flussi di lavoro di esportazione o importazione dei file.
Inoltre, una nuova opzione Study-dependent input nello studio Surrogate Model Training consente di includere nei dati di addestramento i risultati di sweep in funzione del tempo o della frequenza. Ciò semplifica l'incorporazione di dati dinamici o dipendenti dalla frequenza nei modelli surrogati.
Ottimizzazione
Tipo di solutore adjoint discreto
È disponibile un nuovo tipo di solutore Time discrete adjoint per il controllo ottimale e la stima dei parametri dipendenti dal tempo. Questo tipo di solutore si basa su un metodo di sensibilità discreta, che offre una maggiore robustezza, una migliore precisione e prestazioni più rapide per l'ottimizzazione basata sul gradiente con il Time-Dependent Solver.
Nei problemi di stima dei parametri transitori, si ottengono miglioramenti significativi in termini di velocità con i solutori SNOPT (Sparse Nonlinear Optimizer) o IPOPT (Interior Point Optimizer). Ciò è dovuto al fatto che la sensibilità aggregata dell'intero obiettivo viene calcolata in un unico passaggio, invece di calcoli separati per ogni punto di misura. Il precedente metodo di sensibilità continua è ancora disponibile, ma non è più quello predefinito per l'ottimizzazione transitoria.
Entrambi i metodi, discreto e continuo, riducono il consumo di memoria grazie al checkpoint, che comporta il ricalcolo della soluzione di partenza. Inoltre, c'è una nuova opzione Out-of-core che può essere utilizzata in alternativa per la gestione della soluzione previsionale, che invece utilizza lo spazio temporaneo su disco per evitare la ricomputazione.
Ottimizzazione globale efficiente
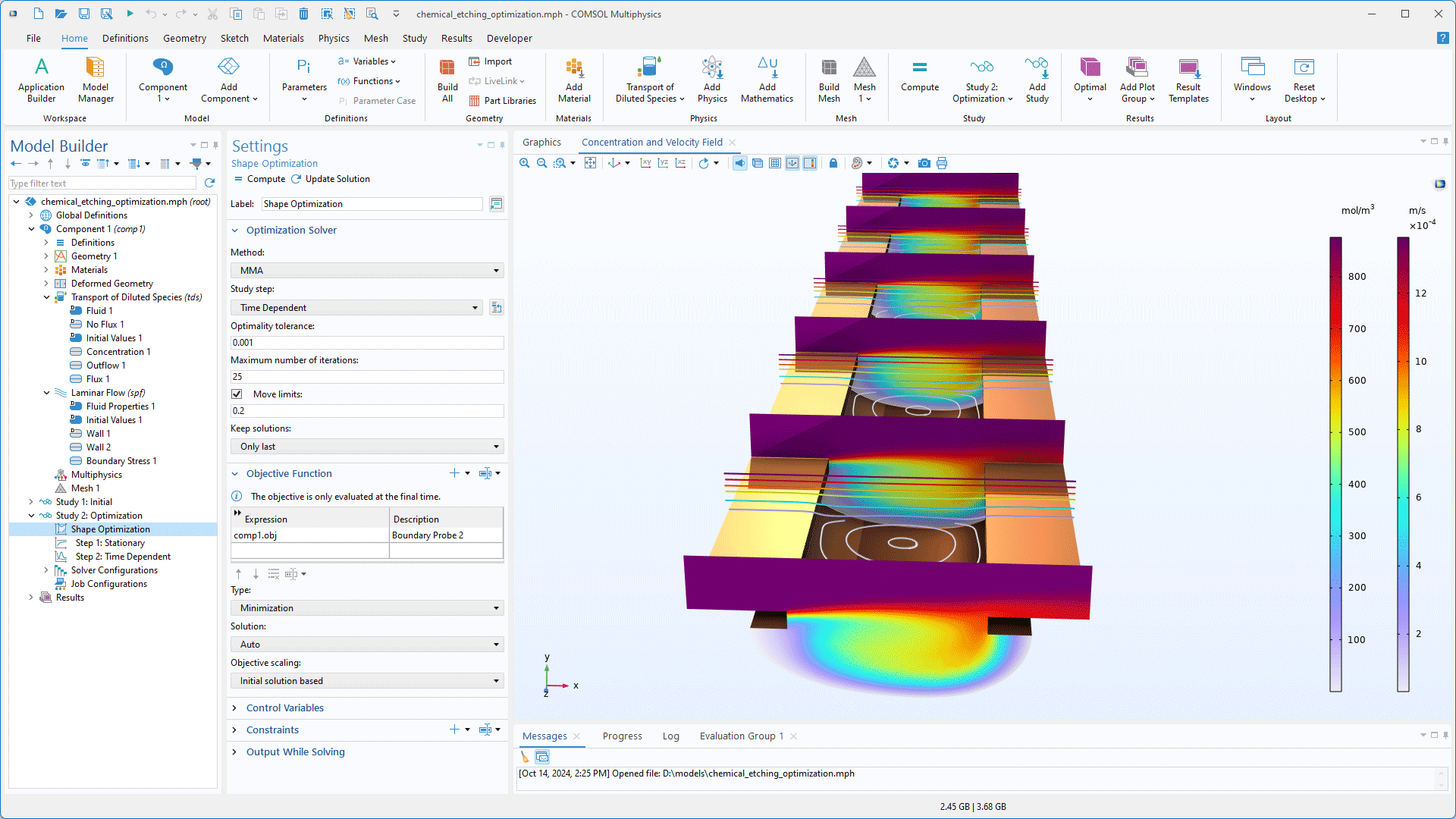
È stato introdotto un nuovo solutore di ottimizzazione senza gradiente che utilizza l'algoritmo di ottimizzazione globale efficiente (EGO). Questo solutore è particolarmente adatto ad affrontare problemi di ottimizzazione con diversi optima locali, in quanto non richiede un'ipotesi iniziale per i parametri di controllo ed è meno incline a rimanere intrappolato in un minimo locale, il che lo rende particolarmente utile per problemi di ottimizzazione impegnativi, come quelli che si incontrano nelle analisi nel dominio della frequenza.
Sebbene il solutore EGO sia più lento dei metodi di ottimizzazione locale a causa della sua strategia di ricerca globale, fornisce una preziosa robustezza nella navigazione di paesaggi risolutivi complessi. Dopo aver eseguito il solutore EGO, si raccomanda di elaborare ulteriormente i risultati utilizzando un metodo di ottimizzazione locale per perfezionare la soluzione. Inoltre, il solutore consente di ispezionare il modello surrogato utilizzato per l'analisi, fornendo ulteriori informazioni sul processo di ottimizzazione.
Risolutore di autovalori non lineari e ordinamento migliorato
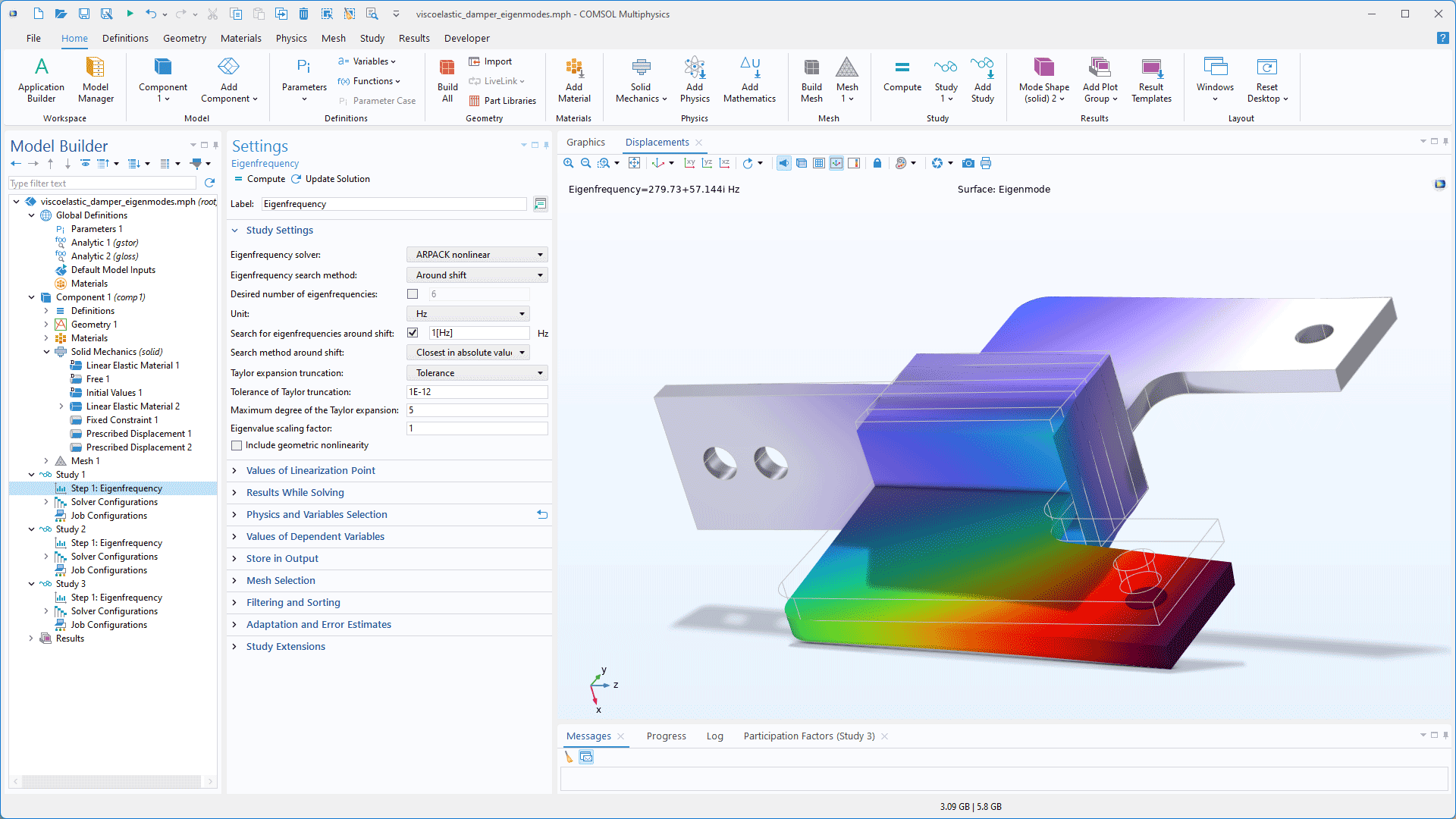
Un nuovo risolutore per autovalori non lineari basato sulla libreria ARPACK è ora disponibile come opzione all'interno del risolutore di autovalori, eliminando la necessità di iterazioni manuali quando si risolvono autovalori non lineari. Ciò è utile per l'analisi strutturale con materiali viscoelastici, l'analisi dei modi elettromagnetici e altro ancora.
Inoltre, è stata aggiunta una nuova sezione Filtering and Sorting alle impostazioni delle fasi di studio Eigenvalue, Eigenfrequency e Boundary Mode Analysis. In questo modo è possibile applicare espressioni di filtro, come real(freq) + 1e-6 > 0, e ordinare le soluzioni agli autovalori in base a vari criteri, come le parti reali o immaginarie, le loro grandezze o i valori assoluti, in ordine crescente o decrescente. Le opzioni di ordinamento sono disponibili anche nei nodi funzionali Eigenvalue Solver e Combine Solutions quando si lavora con soluzioni di tipo autovalore.
Modello di ordine ridotto a decomposizione ortogonale (POD)
È stata aggiunta una nuova tecnica di riduzione del modello, la POD. L'idea principale di POD è quella di utilizzare le istantanee di un modello per eseguire una decomposizione di un campo fisico utilizzando le idee dell'analisi delle componenti principali. Il POD può essere utile per i problemi che sono parametrizzati nel dominio della frequenza.
Miglioramenti al solutore
Tolleranza adattiva per i solutori lineari
Quando si risolvono problemi non lineari, è ora possibile far variare in modo adattivo la tolleranza del solutore lineare. Ciò può portare a sostanziali accelerazioni. Questo metodo utilizza la stima degli errori del solutore non lineare per risolvere con una minore precisione quando si è lontani dalla soluzione e con una maggiore precisione quando ci si avvicina alla convergenza. La tolleranza adattativa nel solutore lineare è supportata per il metodo di smorzamento Constant. È inoltre supportata insieme al metodo pseudo-time-stepping, molto diffuso per i problemi CFD stazionari.
Scalatura per il metodo multigrid algebrico (AMG)
La scalatura delle righe per il metodo AMG può ora essere determinata automaticamente. Abilitando Row equilibration nel nodo Advanced del nodo Stationary Solver si ottiene la selezione automatica di una scala appropriata per il solutore multigrid.
